1.  前の記事
2. 次の記事 

読者からの質問です．


仮に ２本の無限長の平行直線電路間の相互誘導について という条件で解説してみたいと思います．もし条件がずれていると思われたら 再度投稿ください．

［条件］
　　平行電路の間隔：d[m]
　　電路長：L[m]
　※条件とする電路長Lは，無限長の長さから相互誘導を対象とする部分の長さとします．



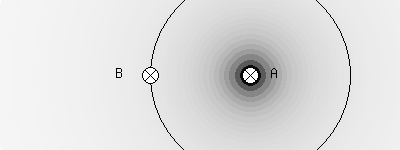
上図は，画面に対して垂直の方向に電路Ａ，Ｂが２本平行に置かれた状態です．ここで，Ａにのみに電流I[A]が流れるものとします． その時の，電路Ａの周囲に分布する磁束は次式の関係にあります．（無限長直線電路のつくる磁束密度はこちら参照）

　　

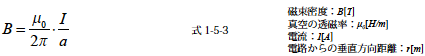
上式における a は，電路Ａからの距離です．この式で示す，磁束密度 Bの分布を上図に示しています．ここで，電路Ａ，Ｂ間の 相互インダクタンスを考えます．相互インダクタンスは， 一次回路に流れる電流のつくる磁束が，二次回路に対して鎖交する磁束です．詳しくは，↑リンク参照．

よって，２本の無限長の平行直線電路間の相互インダクタンスは，一次回路をＡとすると二次回路Ｂに鎖交する磁束は，上図で言うＡを 中心にＡ−Ｂ間を半径とする円の外側であることがわかると思います．

よって，Ｂへの鎖交磁束は，

　　

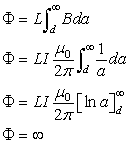
ということになります．この鎖交磁束Φは，相互インダクタンスと等価です．∞の相互インダクタンスでは，現実にそぐわないですよね． 実際，我々が電子回路として電路を構成する場合には，必ず電流の復路があるんですね．常に回路は環状になりますから．ですから， 現実にそぐわない回路を計算した結果が，やはり現実にそぐわない解として導き出されている訳です．

---

ここで，画面と垂直にもう一本電路Ｃが復路として存在する場合を考えます．

［条件］
　　電路Ａ，Ｂ間の間隔：d1[m]
　　電路Ｂ，Ｃ間の間隔：d2[m]
　　電路長：L[m]
　※条件とする電路長Lは，無限長の長さから相互誘導を対象とする部分の長さとします．

　　

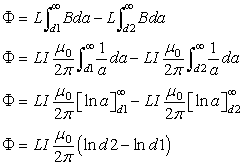
解き方は，前半の方法を踏襲して，電路Ａと電路Ｃの影響を重ねの理によって合成しています． この鎖交磁束Φは，ＡＣ電路とＢ電路との相互インダクタンスと等価です．仮にこの相互インダクタンスをＭとすると電路Ｂに 励起される誘導電圧は

　　M=Φ
　　

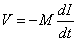
となります．