1.  前の記事
2. 次の記事 

読者からの質問です．


まず，式2-2-44について

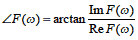　　　　式2-2-44

この式は，伝達関数F(s)の周波数応答F(ω)について，複素平面における位相角を算出しています．下図で，位相角について図示して います．

　　

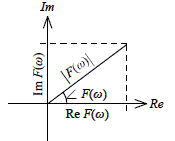
∠F(ω)は，幾何学的な視点では，0〜360°の範囲になります．しかし，ここでの位相角は，単に幾何学的な 角度を求めているものではなく正弦波応答について基準と応答波形との遅延時間を，正弦波周期を基準360°として角度換算したもの です．ちなみに，正弦波応答の遅延時間は位相遅延といいます， こちらで詳しく解説していますのでご参照ください．

よって，正弦波周期以上の位相遅延が生じていれば，360°以上にもなります．ご質問にあるように，90°までの範囲というのは， コンピュータによって算出した場合の話だと思います．数学上の話であれば，式2-2-44で過不足無いと考えています．

---

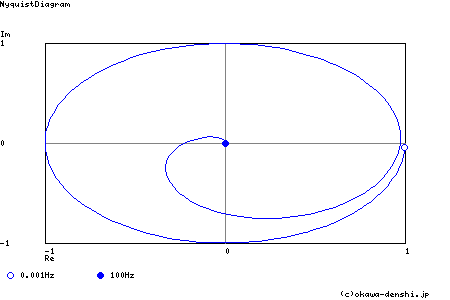
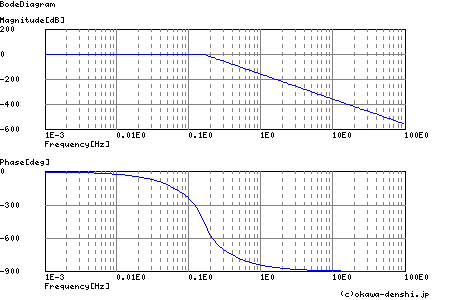
下図は，正規化（ω=1[rad/s]）10次バターワース・ローパス・フィルタのナイキスト線図とBode線図です．下図ナイキスト線図は，上記で言う F(ω)の複素平面上における ω または f 変化時の軌跡を示しています．下図では，0.001Hzから100Hzまでの範囲のF(ω)の軌跡を 示しています．

ここで，式2-2-44で定義されている∠F(ω)は，実数軸との角度（位相：phase）を示しています．その位相を示したものが， ナイキスト線図の下のBode線図におけるphase（位相特性）になります．図の場合，位相角は f=0Hz に近いほど 0°に近く，fが大きく なるに従って位相角が大きく開いていくことが図から読みとることができるかと思います．また，この軌跡を追う限り90°を挟む推移に おいてもリニアに位相角が変化することも読みとることができると思います．