F(ω) の大きさと位相について
時間関数をフーリエ変換をすると,その時間関数に含まれる振動成分の周波数と大きさの関係を示す周波数関数が得られます.その周波数関数は,実数と虚数を含む複素数として得られます.ここでは,実数の周波数または虚数の周波数とはどのような意味があるのかを考えます.
フーリエ変換によって得られる周波数関数F(ω) は実数部と虚数部によって構成されますので,次式のように示すことができます.
| F(ω)=Re F(ω)+j Im F(ω) | 式2-2-42 |
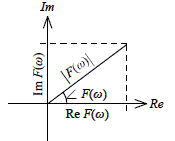
図2-2-13 複素平面におけるF(ω)
図2-2-13は上式の関係を複素平面上に示したものです.ここでF(ω) の大きさは
| 式2-2-43 |
と示すことができます.これは複素平面(図2-2-13)におけるF(ω)の斜辺の長さをピタゴラスの定理によって求めています.
つづいて図2-2-13 における角度∠F(ω)はF(ω)の位相を示しています.数式で示すと
| |
式2-2-44 |
となります.
ところでcos波をフーリエ変換すると実数軸上にスペクトルが得られ,sin波をフーリエ変換すると虚数軸上にスペクトルが得られることを示しましたが,このことからも,∠F(ω)は時間関数におけるcos波の要素を基準にF(ω) の位相の進みの大きさを示していることがわかります.