群遅延 (Group delay)と位相の関係
図2-3-33のような伝達関数によってモデル化できる信号伝達系について,入出力間の信号遅延を評価する方法について考えます.
| Vi(s) → | G(s) | → Vo(s) |
図2-3-33 伝達系の例
ここで考える遅延は,図2-3-34に示すような定常的に連続で与えられる正弦波の応答遅延です.
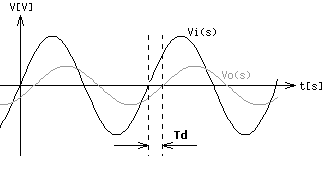
図2-3-34 正弦波信号の遅延
連続正弦波の応答については,以前にも周波数応答のページで触れています.周波数応答では,周波数-ゲイン特性の他に,周波数-位相特性の例を図2-3-35に示しました.その周波数-位相特性は,正弦波の入出力間の遅延時間を正弦波周期(360[deg])を基準として遅延を角度で示したものです.
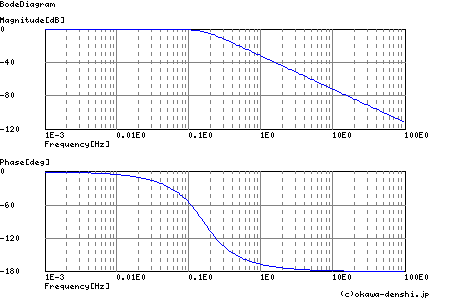
図2-3-35 位相特性(周波数応答)
2次バターワース・ローパス・フィルタω=1rad/sの例
位相と位相遅延
まず,周波数応答における遅延時間Tdを位相角としてを求めてみます.伝達関数G(s)をフーリエ変換するとG(jω).このG(jω)の絶対値がこの伝達関数のωにおけるゲイン(の絶対値)になります(詳細はこちら).位相角は,G(jω)の実数部をRe{G(jω)},虚数部をIm{G(jω)}とすれば次式のようになります.△
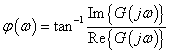
|
式2-3-52 |
φ:位相[rad] ω:角周波数[rad/s] |
図2-3-35のグラフにおける位相(Phase)は,式2-3-52から求められたものです.
つづいて,図2-3-34における正弦波の応答遅延時間Tdは,上式の周波数−位相の関係式から求めていきます.正弦波の1周期が1/fで,1周期時間に対して角度の比からφ(ω)/2πまたはφ(ω)/360ですので下式2-3-53のようになります.(Tdは遅延ですので位相進みに対しマイナスになります)
よって
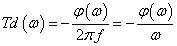
|
式2-3-53 |
Td:位相遅延[s] φ:位相[rad] ω:角周波数[rad/s] |
式2-3-53をグラフに示すと
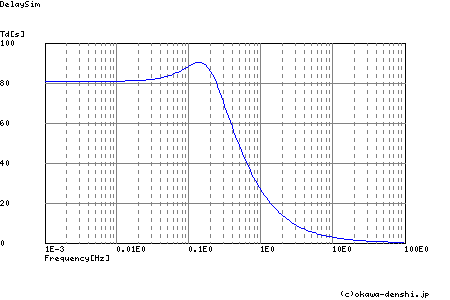
図2-3-36 位相遅延特性
図2-3-36は,正規化バターワース・ローパス・フィルタのTdの算出結果(位相遅延特性)です.
このような単純な周波数-遅延時間の特性は,オーディオ分野など低周波域から高周波域までの伝達系の遅延を広い範囲に適用して評価する際に用いられます.たとえば,音源に低音と高音を含む場合に,伝達系の両者の遅延を均一にすることで音が正しく再現されることになり,伝達系を設計する上での評価に適します.
群遅延
さて,遅延評価に頻繁に利用される 群遅延について解説します.まず,群遅延は次の式2-3-54のように定義されます.Td(位相遅延特性)→式2-3-53との違いは,遅延の絶対値ではなく遅延の対周波数変化(微分型)で示されるところです.
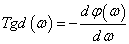
|
式2-3-54 |
Tgd:群遅延[s] φ:位相[rad] ω:角周波数[rad/s] |
式2-3-54をグラフに示すと
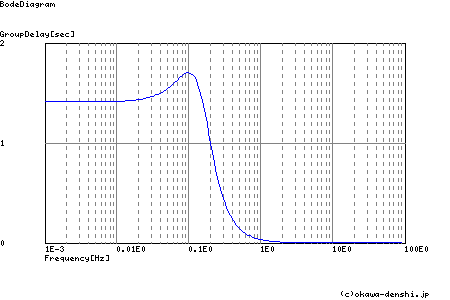
図2-3-37 群遅延特性
微分型で示す群遅延は,図2-3-35に示すような周波数−位相特性における(負の)傾きを求めていることになります.伝達系のTgd(ω)が連続になる条件において,引数ωの値前後の近い周波数を対象に遅延を評価することになります.
位相遅延とは反対に,極限られた周波数範囲のなかで急激に遅延時間が変化する場合の評価に適します.たとえば矩形波のように,複数周波数の正弦波により構成されている波形の場合には,対周波数の遅延変化が大きい系では過渡波形の再現性の壊れが群遅延により評価できます.
たとえば図2-3-37の系についてステップ応答を考える場合,0.1Hz付近の群遅延の増加が読みとれますので,過渡現象において遅延の小さい低周波側の応答波形に0.1Hz付近の遅延波形が重ね合うことになり,その結果としてステップ応答波形がオーバーシュートが起こることが,この群遅延からも読みとることができます.
下図に,図2-3-37の系における伝達関数のステップ応答を示します.青の線が,図2-3-37の系(2次バターワースフィルタ)の応答です.
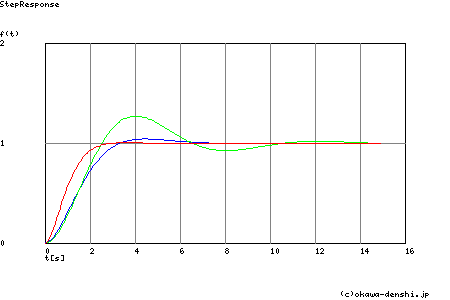
−バターワースフィルタ,−チェビシェフフィルタ,−ベッセルフィルタ
図2-3-39 ステップ応答特性
上図2-3-39のステップ応答波形は,バターワースフィルタの応答の他は,チェビシェフ,ベッセルの2次ローパス・フィルタの応答波形を求めたものです.各フィルタの伝達関数は,右上に記しておきます.これらの伝達関数の群遅延特性は下図のようになります.
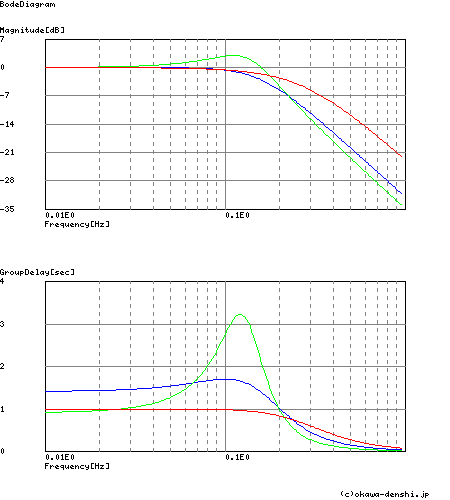
−バターワースフィルタ,−チェビシェフフィルタ,−ベッセルフィルタ
図2-3-38 ゲイン特性と群遅延特性
図2-3-38に示す群遅延の特性のように,狭い範囲の周波数において比較的に群遅延の大きいチェビシェフ・フィルタではやはり,STEP応答波形の壊れが大きく,ベッセル・フィルタのように群遅延が透過域でほぼ一定となる伝達関数の場合には,STEP応答波形の壊れが比較的小さくなる特徴が顕著に現れています.