1.  前の記事
2. 次の記事 

2次CRフィルタ計算ツールに関して，読者からの質問です．



次の2次CRローパス・フィルタを例にあげて解説します．（本サイトで提供している2次CRフィルタツールは，下図のLPFの他，HPF，BPFの ３種あります）

Vi(s)→

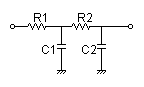
→Vo(s)

伝達関数は，下記の通り．
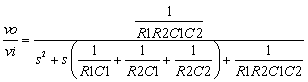　　　---(1)


仮に，下図のようにバッファを介して１次CRフィルタがシリーズに接続している系としてこの2次CRローパス・フィルタを想定して 考えてみます．（注：完全等価の系ではありません）



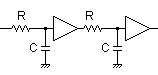
上図フィルタの等価ブロック線図は下図の通りです．

Vi→

2πfc1  s + 2πfc1

→

2πfc2  s + 2πfc2

→Vo

ここでのfc1，fc2は，ブロック線図内で仮想的に用いているパラメータです．fc1は系前段のRCフィルタのカットオフ周波数，fc2は後段の RCフィルタのカットオフ周波数です．

---

ここでご質問にあるように，インピーダンスの低い方から並べた場合と、高い方から並べた場合の差ということで，下表のように インピーダンスの高低および低高の条件設定をシミュレーションした結果を比較してみました．

設定	条件	カットオフ周波数	減衰比
A	R1 = 10kΩ C1 = 0.01uF R2 = 1kΩ C2 = 0.1uF	f1 = 133.56317345[Hz] f2 = 18965.0299976[Hz]	ζ = 6 (Q = 0.0833333333333)
B	R1 = 1kΩ C1 = 0.1uF R2 = 10kΩ C2 = 0.01uF	f1 = 1161.58246566[Hz] f2 = 2180.67133927[Hz]	ζ = 1.05 (Q = 0.47619047619)

上記のA，Bの設定におけるBode線図を示します．【条件】A:水色− ，B:青− です．



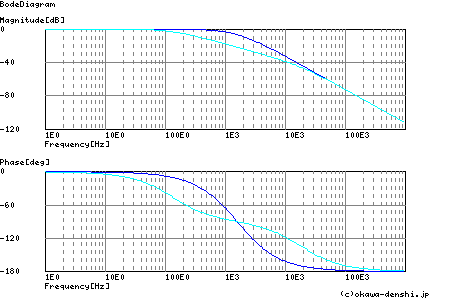
Ａ，Ｂのそれぞれの条件では，結果が異なります．Ａの設定では，２つのカットオフ周波数の値が離れBode線図上で２度曲折しています． Ｂの設定では，２つのカットオフ周波数の値が比較的近くBode線図上では１度曲折しているように見え， 臨界減衰応答に近い設定になります．

通常２次フィルタの設定としては，できるだけ臨界（ζ = 1 あるいは fc1 = fc2） に近い条件がフィルタとしては使いやすいと思います．しかし，このフィルタでは，臨界に限りなく近づけることはできても，臨界その ものの設定にすることはできません．（バッファを介せば臨界設定可能）

そこで，なるべく臨界に近づけるためには，R1，C1のインピーダンスを小さく（R1：小，C1：大）して，R2，C2のインピーダンスを大きく （R2：大，C2：小）とすることで設定できます．

---

つづいて，等価ブロック線図におけるfc1，fc2 について R1，R2，C1，C2 との関係を求めてみます．2次CRローパス・フィルタの極が， fc1，fc2 に対応しますので，伝達関数 式(1)の［分母］= 0 から ２次方程式の解より求めていきます．