20081009
オペアンプを使った高次バターワース・フィルタおよび高次チェビシェフ・フィルタの設計方法 - 2 -
前回の記事では,オペアンプを使ったSallen-Key・フィルタ回路によって5次バターワース・フィルタを設計しました.今回も引き続き, 伝達関数から導き出された数学上のフィルタを,アナログ回路を使って,現実のフィルタ回路(今回はチェビシェフ・フィルタ回路)の設計方法を解説します.
チェビシェフ・フィルタ
チェビシェフ・フィルタの設計もバターワースの方法と同様,特性周波数とゲイン・リップルの条件から伝達関数の極を最初に算出して いきます.その極位置からフィルタを構成する各2次フィルタ(と1次フィルタ)のカットオフ周波数ωおよび減衰比ζを算出して いきます.チェビシェフ・フィルタの場合,構成する各2次フィルタのカットオフ周波数ωは,バターワースのように同じ一定値ではありません. カットオフ周波数ωおよび減衰比ζは,次数に対する関係だけではなくゲイン・リップルの要素も関係していて,簡単な2次元テーブル によって表記することはできません.そこで,ゲイン・リップルを限定して一部を下表に示します.ゲイン・リップルやその他条件を すべて網羅するカットオフ周波数ωおよび減衰比ζの計算ツールは,チェビシェフ・フィルタの特徴 に掲載していますのでこちらも併せてご利用ください.
【ゲイン・リップル1dB】
|
【ゲイン・リップル3dB】
|
上記表の各カットオフ周波数ωは,正規化された(特性周波数1[rad/s])チェビシェフ・フィルタの条件における値を示します. 通常,これらの各ωはフィルタの特性周波数に応じて換算して使用します.たとえば,特性周波数 f[Hz]のチェビシェフ・フィルタに ωを換算する場合には,
ωx = ω × 2πf
fx = ω × f
とします.
上記表に記載のリップル・ゲイン値以外のωやζ は,チェビシェフ・フィルタの特徴のツールから入手できますのでご使用ください.
■多重帰還型フィルタによってチェビシェフ・フィルタを設計する
前回バターワース・フィルタの設計ではSallen-keyを使用しましたので,ここでは多重帰還型フィルタを使ってチェビシェフ・フィルタを 設計します.
偶数フィルタの場合は,2次フィルタであるオペアンプによる多重帰還型フィルタの組み合わせで実現できますが,奇数フィルタの場合は, バターワース・フィルタと同様,最終段に1次フィルタであるCRフィルタを配置します.
[偶数]
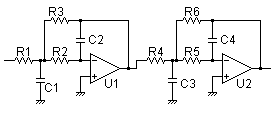
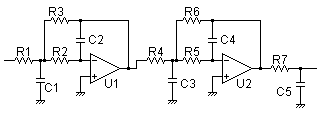
●特性周波数1kHz,ゲインリップル1dBの5次チェビシェフ・フィルタ設計例
ここでは,カットオフ周波数1kHz,ゲインリップル1dBの5次チェビシェフ・フィルタの設計例を示します. 設計条件であるカットオフ周波数fc=1kHzと,減衰比ζは上表の値を使って各フィルタを算出していきます.
U1の系について
fc=1kHz×0.655 ζ=0.357の条件を与えたときのRおよびCの算出
多重帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
R1 = 3.6kΩ
R2 = 11kΩ
R3 = 3.6kΩ
C1 = 0.22uF
C2 = 0.0068uF
遮断周波数(カットオフ周波数)
fc = 653.893080853[Hz]
f=0Hzにおける利得
Gpk = -1[倍] (0)[dB]
クオリティ・ファクタ
Q = 1.39818459141
減衰比ζ
ζ = 0.357606572889
極
p = -233.83646368 +610.652658588i[Hz]
|p|= 653.893080853[Hz]
p = -233.83646368-610.652658588i[Hz]
|p|= 653.893080853[Hz]
位相余裕
pm= 240.8[deg] (f =797.8[Hz])
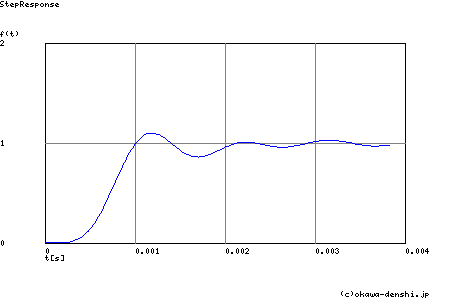
過渡波形に含まれる振動周波数は
f = 610.652658588[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = -1.3 (t =0.00082[sec])
第2ピーク gpk = -0.91 (t =0.0016[sec])
第3ピーク gpk = -1.03 (t =0.0025[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = -1
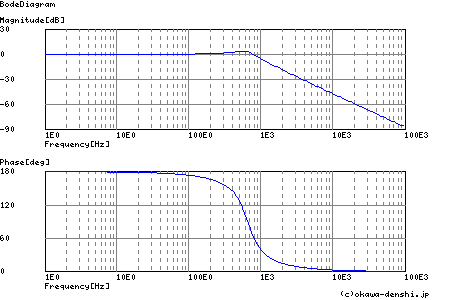
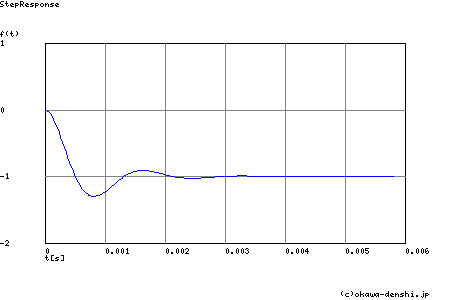
多重帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
| G(s)= |
-16880030.249 s2+2938.47566575s+16880030.249 |
R1 = 3.6kΩ
R2 = 11kΩ
R3 = 3.6kΩ
C1 = 0.22uF
C2 = 0.0068uF
遮断周波数(カットオフ周波数)
fc = 653.893080853[Hz]
f=0Hzにおける利得
Gpk = -1[倍] (0)[dB]
クオリティ・ファクタ
Q = 1.39818459141
減衰比ζ
ζ = 0.357606572889
極
p = -233.83646368 +610.652658588i[Hz]
|p|= 653.893080853[Hz]
p = -233.83646368-610.652658588i[Hz]
|p|= 653.893080853[Hz]
位相余裕
pm= 240.8[deg] (f =797.8[Hz])
過渡波形に含まれる振動周波数は
f = 610.652658588[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = -1.3 (t =0.00082[sec])
第2ピーク gpk = -0.91 (t =0.0016[sec])
第3ピーク gpk = -1.03 (t =0.0025[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = -1


U2の系について
fc=1kHz×0.994 ζ=0.0900の条件を与えたときのRおよびCの算出
多重帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
R4 = 4.53kΩ
R5 = 12.1kΩ
R6 = 4.53kΩ
C3 = 0.47uF
C4 = 0.001uF
遮断周波数(カットオフ周波数)
fc = 991.583785482[Hz]
f=0Hzにおける利得
Gpk = -1[倍] (0)[dB]
クオリティ・ファクタ
Q = 5.58669663376
減衰比ζ
ζ = 0.0894983266101
極
p = -88.7450894944 +987.604532555i[Hz]
|p|= 991.583785482[Hz]
p = -88.7450894944-987.604532555i[Hz]
|p|= 991.583785482[Hz]
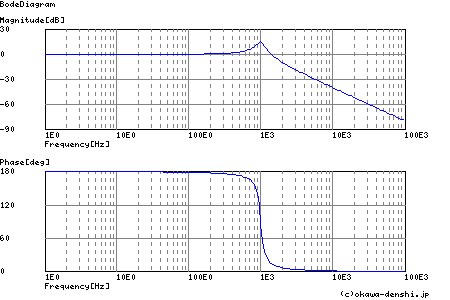
位相余裕
pm= 194.6[deg] (f =1391.4[Hz])
過渡波形に含まれる振動周波数は
f = 987.604532555[Hz]
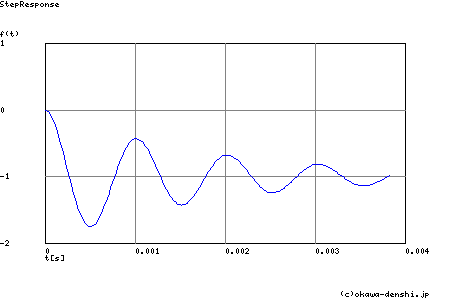
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = -1.75 (t =0.0005[sec])
第2ピーク gpk = -0.43 (t =0.001[sec])
第3ピーク gpk = -1.43 (t =0.0015[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = -1
多重帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
| G(s)= |
-38816696.3032 s2+1115.20368479s+38816696.3032 |
R4 = 4.53kΩ
R5 = 12.1kΩ
R6 = 4.53kΩ
C3 = 0.47uF
C4 = 0.001uF
遮断周波数(カットオフ周波数)
fc = 991.583785482[Hz]
f=0Hzにおける利得
Gpk = -1[倍] (0)[dB]
クオリティ・ファクタ
Q = 5.58669663376
減衰比ζ
ζ = 0.0894983266101
極
p = -88.7450894944 +987.604532555i[Hz]
|p|= 991.583785482[Hz]
p = -88.7450894944-987.604532555i[Hz]
|p|= 991.583785482[Hz]
位相余裕
pm= 194.6[deg] (f =1391.4[Hz])
過渡波形に含まれる振動周波数は
f = 987.604532555[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = -1.75 (t =0.0005[sec])
第2ピーク gpk = -0.43 (t =0.001[sec])
第3ピーク gpk = -1.43 (t =0.0015[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = -1


CR系について
fc=1kHz×0.289の条件を与えたときのRおよびCの算出
CRローパス・フィルタ計算ツールの結果概要
伝達関数:
R7 = 5.6kΩ
C5 = 0.1uF
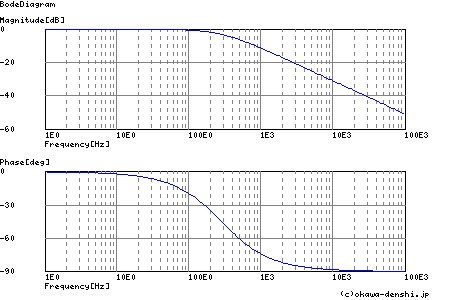
遮断周波数(カットオフ周波数)
fc = 284.205255521[Hz]
極
p = -284.205255521[Hz]
|p|= 284.205255521[Hz]
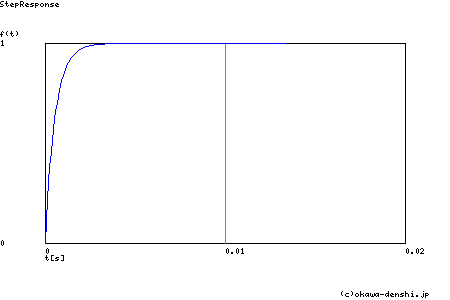
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
CRローパス・フィルタ計算ツールの結果概要
伝達関数:
| G(s)= |
1785.71428571 s+1785.71428571 |
R7 = 5.6kΩ
C5 = 0.1uF
遮断周波数(カットオフ周波数)
fc = 284.205255521[Hz]
極
p = -284.205255521[Hz]
|p|= 284.205255521[Hz]
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1


理想のオペアンプを使ったSPICEシミュレーションを示します.
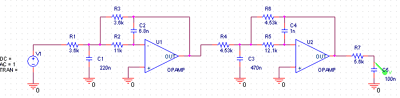
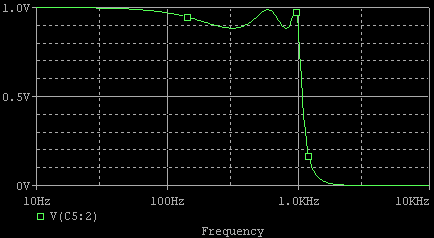
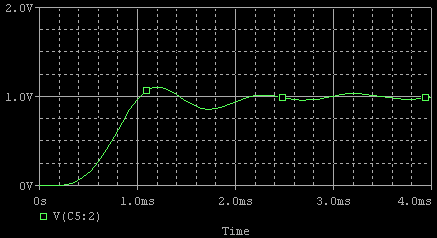
一応5次チェビシェフ・フィルタについて理論伝達関数から求めた特性(チェビシェフ・フィルタの特徴に掲載のツールによるSim) も掲載しておきます.
下図のBode線図と上図の周波数特性とは,縦軸が異なります.下図はLogスケール,上図はリニアスケールです.
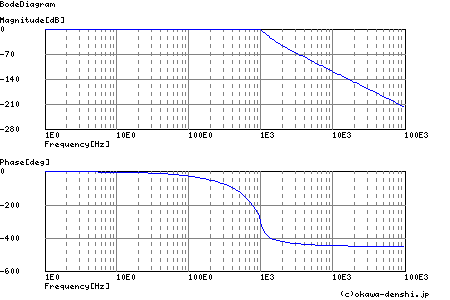
チェビシェフ・フィルタの場合,回路を構成するそれぞれの1次,2次のフィルタのカットオフ周波数がフィルタ全体の特性周波数よりも 低く設定されます.フィルタ全体の特性周波数に向かって減衰が大きくなるところをζを低め(Qを高め)に設定して振動系とし 増幅して減衰を補っています.そのためチェビシェフ・フィルタの特性周波数に近づくほど,構成している2次フィルタは, 低ζ(高Q)に設定されます.
振動系の設計では,前回も解説していますが,振動のオーバーシュート,アンダーシュートが同相電圧範囲を超えない設計にするよう 注意が必要です.さらに,チェビシェフ・フィルタ特有のゲイン・リップルの仕様を回路図ベースで確実に実現するためには, ピークゲインの周波数をピンポイントに正しい周波数に高い精度で設定する必要があります.極僅かなズレであっても急峻なゲイン勾配に 積み上げていますのでゲイン・リップルの理論値との差は,一般に大きくなります.
そこで,回路設計上U2の系では,抵抗にE96系列を採用してカットオフ周波数 を理論値に近づけています.しかし,リアルワールドでは,様々な誤差を取り込む必要があり,この有限の精度のなかで ゲイン・リップル,特性周波数等フィルタ仕様を電子回路上に組み込んでいくのは,仕様との折り合いも含めかなり緻密な作業になります.
[記事URL] http://okawa-denshi.jp/blog/?th=2008100900
カテゴリー:フィルタ(20)
カテゴリー:フィルタ(20)
 前の記事
前の記事