20090202
ベッセル・フィルタの特徴
前の記事
ベッセル・フィルタ伝達関数
ベッセル・ローパス・フィルタ伝達関数の定義は次式の通りです．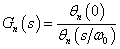
θn(s)は，逆ベッセル多項式になります． 逆ベッセル多項式の詳細はこちらを参照ください．nは， フィルタの次数です．ω0は，フィルタの特性周波数です．
逆ベッセル多項式は，次式の通りです．
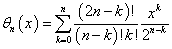
上２式より正規化（ω0=1rad/s）ベッセル・ローパス・フィルタの伝達関数は，
| G1(s)= | 1 s +1 |
| G2(s)= | 3 s2 +3s +3 |
| G3(s)= | 15 s3 +6s2 +15s +15 |
| G4(s)= | 105 s4 +10s3 +45s2 +105s +105 |
| G5(s)= | 945 s5 +15s4 +105s3 +420s2 +945s +945 |
・
・
１次から５次のベッセル・ローパス・フィルタ伝達関数の周波数特性を下図に示します．
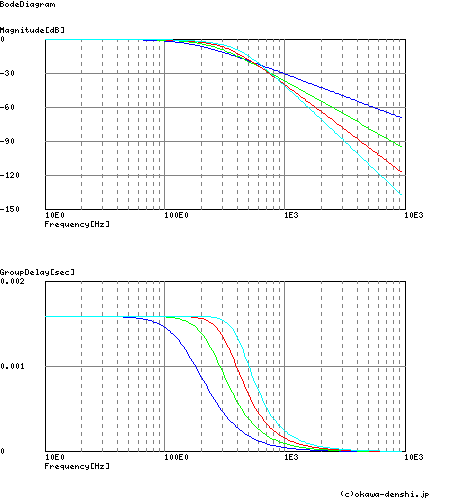
−２次 −３次 −４次 −５次
|
上図は，いずれも100Hzにおける周波数応答と群遅延特性を示しています．バターワース・フィルタ等で設計に用いるカットオフ周波数の
概念で考えれば，次数の大きさに応じてカットオフ周波数の値も大きくなっていく特徴が，この特性から読みとることができます． そこのところはベッセル・フィルタを設計する上で大いに注意する点です．ベッセル・フィルタ伝達関数の定義から，このような フィルタの特性周波数とカットオフ周波数のミスマッチが起こります．簡単に言うとベッセル・フィルタの次数が大きくなっても 特性周波数から遮断域の帯域において遮断特性が向上せずにむしろ悪くなる傾向があります．このような特徴は，設計上知っていること は，たいへん重要です． 詳細のベッセル・ローパス・フィルタのシミュレーションはこちらのツールで実施できます． ■n次ベッセル・ローパス・フィルタのシミュレーション
|
たとえば，特性周波数をω=1[rad/s]，ω=1/2[rad/s]，ω=1/3[rad/s]と振った場合の群遅延を見てみましょう．
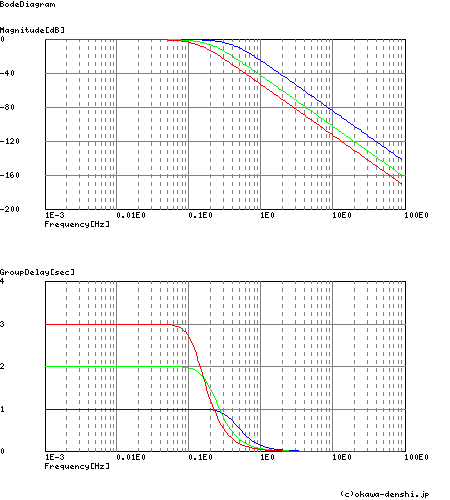
−ω=1[rad/s] −ω=1/2[rad/s] −ω=1/3[rad/s]
上図（GroupDelay）の縦軸の要素（群遅延値）に着目すると，ベッセル・フィルタの透過域における群遅延の値は， 次式のように特性周波数ωの逆数に等しいことがわかります．
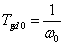
よってベッセル・フィルタは，信号伝達において，透過域の広い周波数帯域の信号を，群遅延の値をほぼ一定に遅延させる高域遮断の伝達 システムであることがわかります． そのため，群遅延の設定値TGD0[s]によって，ベッセル・フィルタの伝達関数を設計する ことも可能な訳です．
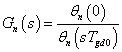
どちらかといえばこちらの方が，ベッセル・フィルタの思想概念を反映しているようにも思います．
ベッセル・フィルタ，バターワース・フィルタ，チェビシェフ・フィルタの各 群遅延特性と各フィルタのステップ応答波形（の壊れ）の シミュレーションをこちらに掲載していますのでご参照ください．