20090126
ベッセル多項式
前の記事
ベッセル多項式
まず，ベッセル多項式とは次式に示すような多項式です．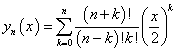
この式を，展開して示すと
y0(x)=1
y1(x)=x +1
y2(x)=3x2 +3x +1
y3(x)=15x3 +15x2 +6x +1
y4(x)=105x4 +105x3 +45x2 +10x +1
y5(x)=945x5 +945x4 +420x3 +105x2 +15x +1
y6(x)=10395x6 +10395x5 +4725x4 +1260x3 +210x2 +21x +1
y1(x)=x +1
y2(x)=3x2 +3x +1
y3(x)=15x3 +15x2 +6x +1
y4(x)=105x4 +105x3 +45x2 +10x +1
y5(x)=945x5 +945x4 +420x3 +105x2 +15x +1
y6(x)=10395x6 +10395x5 +4725x4 +1260x3 +210x2 +21x +1
逆ベッセル多項式
つづいて逆ベッセル多項式は，次のように定義されます．θn(x) = xn yn(1/x)
よって
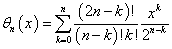
上式を展開すると
θ0(x)=1
θ1(x)=x +1
θ2(x)=x2 +3x +3
θ3(x)=x3 +6x2 +15x +15
θ4(x)=x4 +10x3 +45x2 +105x +105
θ5(x)=x5 +15x4 +105x3 +420x2 +945x +945
θ6(x)=x6 +21x5 +210x4 +1260x3 +4725x2 +10395x +10395
θ1(x)=x +1
θ2(x)=x2 +3x +3
θ3(x)=x3 +6x2 +15x +15
θ4(x)=x4 +10x3 +45x2 +105x +105
θ5(x)=x5 +15x4 +105x3 +420x2 +945x +945
θ6(x)=x6 +21x5 +210x4 +1260x3 +4725x2 +10395x +10395
逆ベッセル多項式は，ベッセル多項式とは係数の付き方が反対になります．