1.  前の記事
2. 次の記事 

３次方程式の根−カルダノ法による３つの実数根についてのメモです．一般のｎ次方程式の根を求めるには，こちらの計算ツールでどうぞ．

カルダノ法によって３次方程式の根を求めると，３つの実数解が得られる条件において３乗根の中に虚数を含む式に計算を阻まれる状態に なります．数学的にはまったく問題無いのですが電算には適さないので，ここで複素数のn乗(根)について実部，虚部に展開しておこうと いうメモ的な記事になります．

　　x³+a₁x²+a₂x+a₃ = 0

上式の方程式の根は，カルダノ法という方法によってxを代数的に求めることができます．その根の公式は次の通り．

　　

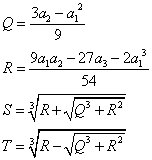
上式としたとき方程式の根は次式の通り

　　

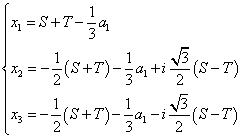
ここで
　　D = Q³ +R²

とすると

1. D > 0 : １つの実数根と２つの複素数根
2. D = 0 : ２つの実数根，うち１つは重根
3. D < 0 : ３つの実数根

---

ここで上の３番目の条件D < 0が，すべて実数解をもつにもかかわらず，３乗根の中に虚数を含む式が登場してしまいます．complexライブラリをもつ 言語では，そのまま計算できますが，標準の表計算ソフトなんかでは，計算できないと思いますので，D < 0 条件 におけるその後の展開をメモしておきます．
一般式として次式を求めていきます．

　　(a + ib)^x　　　　　---(1)

ただし，a,b,xは実数．
括弧内を極座標に変換します．

　　a + ib = r(cosθ + isinθ)

rおよびθは
　　
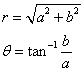
※tan^-1は，360degの範囲で適応できないので，各象限にθを要補正．

オイラーの関係式より

　　cosθ + isinθ = e^iθ

よって(1)は

　　(a + ib)^x = r^xe^ixθ
　　= r^x(cosxθ + isinxθ)

ということで，実部，虚部に展開できました．

---

ここで，D < 0 におけるS,T は
　　

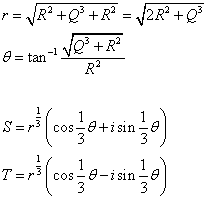
すると，３つの実数根x₁，x₂，x₃は 根の公式より

　　

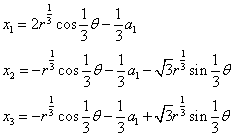
Dによる条件分岐で使い分ける．．．以上，自分用メモでした．