1.  前の記事
2. 次の記事 

伝達関数設計支援ツールの2次系複素数極の配置に関して，２種類のフォームがあります．

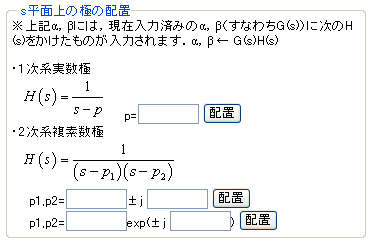
それらの相違（複素数 Re±jIm と A exp ±jθの関係）を教えてください．

---

両者は複素平面上の同一点を異なる方法で示しています．複素面における両者の関係を図示すると



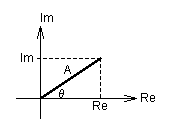
ちょうど２次元座標の直行座標と極座標の表示方法の違いのようなものです．
数式を用いて示すと，A exp jθはオイラーの関係式より

　　A exp jθ＝A(cosθ＋jsinθ)

と示すことができます．よってRe，Imはそれぞれ

　　Re＝A cosθ
　　Im＝A sinθ

となります．


[20080713]追記：
大切なこと言い忘れていました．物理系２次伝達関数の極は，振動系の場合 s 平面上で必ず実数軸を挟んで線対称に２点配置されます． 上に示す極p1，p2の入力フォームには，虚部だけが±として入力が要求されのは，そのような制限があるためです．

それでは，なぜ実数軸線対称に配置されるのか？２次伝達関数の一般式から極を求めてみましょう．

　　

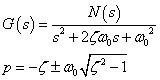
ζ<1 この条件（ルート内マイナス）のときに，振動系になります． 極 p の式からも実数軸に対し線対称に配置されることが読みとれます．これには，ω₀やζが，実数のパラメータであることが 必須の条件になります．つまり，物理系の伝達関数を形成する上で当然の条件が求められ，逆にこれら物理系に虚数設定はありません ので，極が s 平面上で必ず実数軸を挟んで線対称に２点配置されることになります．


あと，一部誤記訂正がありました（現在訂正済みです）
　誤：A exp jθ
　正：A exp ±jθ