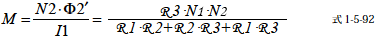磁気回路3
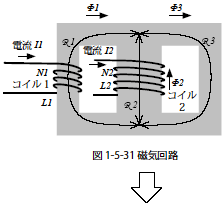
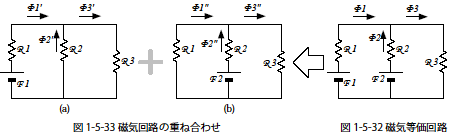
図1-5-31 の相互誘導のある磁気回路について,各コイルの自己インダクタンスと相互インダクタンスを算出します.磁気回路は,図1-5-32に示す電気回路のように磁気抵抗を抵抗に,磁位差を電位差に変換することができます.
このように等価的に示される回路からキルヒホッフの法則,重ね合わせの理や鳳テブナンの定理などの法則を使って各磁気抵抗や磁位差を求めることができます.
図1-5-32のモデルを重ね合わせの理を使って,各コイルがつくる磁束の影響に分解します.図1-5-33(a) はコイル1が磁気回路に与える影響を,図1-5-33(b)はコイル2が磁気回路に与える影響を示します.それぞれの自己インダクタンス(L1,L2)は図1-5-33 (a),(b)のそれぞれの系から求めることができます.
たとえばL1を求めてみましょう.L1は単位電流あたりのコイル1への鎖交数です.まず最初にコイル1の影響による磁束数Φ1' を求めます.
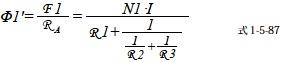
式中のR A はコイル1 から見た磁気回路の合成磁気抵抗になります.よってコイル1の自己インダクタンスL1は
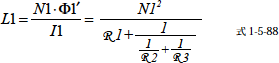
と求めることができます.つづいてコイル2の自己インダクタンスはコイル1のインダクタンスと同様,単位電流あたりのコイル2 への鎖交数なので,コイル2の影響による磁束数Φ2" を求めます.

式中のRA2 はコイル1 から見た磁気回路の合成磁気抵抗になります.よってコイル2 の自己インダクタンスL2 は
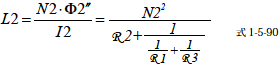
と求めることができます.
次に相互インダクタンスM を求めます.M はコイル1 電流の単位電流あたりにつくられる磁束のコイル2 への鎖交磁束なのでこの磁気回路の場合,Φ2' に相当しますのでこれを求めます.
図1-5-32からのΦ2' の求め方は,鳳テブナンの定理のセクションを参照してください.
![]()
この磁気回路の場合相互インダクタンスをM とするとつぎのようになります.