窓関数
このセクションでは,フーリエ変換によって得られる周波数特性について測定分野などで得られる結果と,実波形に本来構成されている周波数成分(周波数関数)との相関を数学的に検証します.
すでに述べていることですが,フーリエ変換は,t[-∞,∞] の時間範囲を対象とするため実測のように時間を有限長に限定する場合,本来得たい周波数特性とは異なります.たとえば直流のみの波形についてフーリエ変換した場合,あるいは正弦波をフーリエ変換した場合,線状のスペクトルとなりますが,有限時間を切りだした場合,図2-2-3,図2-2-4,図2-2-5のように線状スペクトルにはなりません.
ここでフーリエ変換後の周波数特性からどのような情報を読み解くことができるのか.という観点で考えます.たとえば
- 波形に含まれる振動波形の周波数について精度良く知りたい
- 波形に含まれる振動波形の振幅を精度良く知りたいなど.
実はこうした目的に応じて,フーリエ変換前の時間波形の切り出し方を工夫することで様々な周波数特性をあつらえることができます.
これまで,直流成分,cos波成分,sin成分について無限時間の中から次のような矩形形状に切り出した上でフーリエ変換をしてきました.
ここでは,時間関数f(t)がt[-∞,∞]で連続する関数であるものとして,f(t)とは別に有限時間長に切り出す関数g(t)を考えます.たとえば,これまでのようにf(t)を矩形形状に切り出す場合
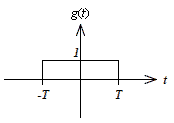
図2-2-6 窓関数の例(Rectangular)
 |
g(t) = 1 (-T≦ t ≦ T) |
| g(t) = 0 (t< -T,t>T) |
このように時間関数の切り出し方は,g(t) = 1 (-T≦ t ≦T)の一通りではなく様々な関数によって切り出すことができます.
このように無限に継続している時間関数の中で,ある有限の時間に,ある特定の形状によって切り出す関数(上記のg(t))を窓関数といいます.窓関数は電子回路設計でもおなじみの測定器FFTなどでも何種類か用意されていることが一般的です.
代表的なものとして
- Rectangular
- Hanning
- Flattop
回路設計でも多用されるフーリエ変換技術.測定分野など有限時間を切り出す必要があるためフーリエ変換には窓関数もをいくつか使用するとそれぞれ異なる周波数特性が得られます.今何を測定しているのかということを数学的に知っておくことが重要です.
また窓関数は,測定分野だけでなく直接的にデジタル信号処理にも広く応用されています.(フーリエ,ラプラスは,びっくりするような所にも応用されています).ちょっと基礎を知っていれば独自に窓関数を設定し,様々な周波数関数にカスタマイズし得たいパラメータを自在に抽出できる利点があります.