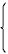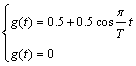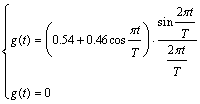窓関数2
FFT(測定器)等で使用される窓関数について,フーリエ変換後に得られる周波数関数の特徴を捉えます.窓関数を用いたフーリエ変換の定義は,時間関数をf(t),窓関数をg(t)とすると次のように与えられます.
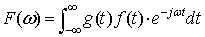 式2-2-27
式2-2-27
ここで,次の窓関数を適用してフーリエ変換していきます.
| 窓関数名 | 窓関数 | |||
| Rectangular |
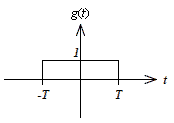 図2-2-6 窓関数 Rectangular
式2-2-28 |
|||
| Hanning |
 図2-2-7 窓関数 Hanning
式2-2-29 |
|||
| Flattop |
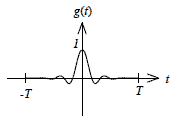 図2-2-8 窓関数 Flattop
式2-2-30 |
すべての関数は,DC成分,sin 成分,cos 成分に分解できるので,
- f(t) = v
- f(t) = v cos ω0t
- f(t) = v sin ω0t
上記の3種の時間関数を例にして,それぞれの窓関数を使ってフーリエ変換していきます.
時間関数f(t) = vのフーリエ変換
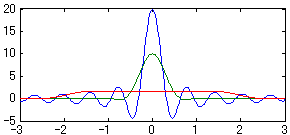
図2-2-9 f(t)=vの各窓関数を用いたフーリエ変換
緑:Hanning
赤:Flattop
T=10s
v=1V
| 窓関数 | 周波数関数 F(ω),ピーク,幅 |
| Rectangular | 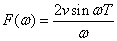 式2-2-31
式2-2-31
F(ω)のピーク値 :2vT
メインローブの幅 :2π/T |
| Hanning |
計算式2-2-32および計算過程はこちら
F(ω)のピーク値 :vT
メインローブの幅 :4π/T |
| Flattop |
F(ω)のピーク値 :vTに比例 |
時間関数f(t) = v cos ω0tのフーリエ変換
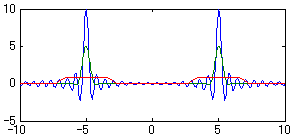
図2-2-10 f(t)=v cosω0tの各窓関数を用いたフーリエ変換
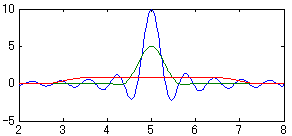
図2-2-10a 拡大図
緑:Hanning
赤:Flattop
T=10s
v=1V
ω0=5rad/s
| 窓関数 | 周波数関数 F(ω)のピーク,幅 |
| Rectangular |
F(ω)のピーク値 :vT
メインローブの幅 :2π/T |
| Hanning |
F(ω)のピーク値 :vT/2
メインローブの幅 :4π/T |
| Flattop |
F(ω)のピーク値 :vTに比例 |
時間関数f(t) = v sin ω0tのフーリエ変換
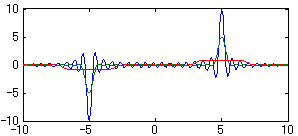
図2-2-11 f(t)=v sinω0tの各窓関数を用いたフーリエ変換
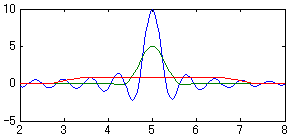
図2-2-11a 拡大図
緑:Hanning
赤:Flattop
T=10s
v=1V
ω0=5rad/s
| 窓関数 | 周波数関数 F(ω)のピーク,幅 |
| Rectangular |
F(ω)のピーク値 :vT
メインローブの幅 :2π/T |
| Hanning |
F(ω)のピーク値 :vT/2
メインローブの幅 :4π/T |
| Flattop |
F(ω)のピーク値 :vTに比例 |
電子回路設計でもおなじみのFFTにもよく使われているRectangular,Hanning,Flattopの代表的な窓関数について特徴を知っておきましょう.
FFTを使う際多くの場合,信号に含まれる周波数成分の切り分けやその周波数成分の相対的な大きさを知ることが目的となります.
上記の時間関数の例では,DC成分,cos波やsin波など波形の基本構成要素として取り上げました.これらの関数は,いずれも-∞〜∞のフーリエ変換で,線状のスペクトルの周波数関数をつくります.
たとえば測定の分野で周波数の切り分けを行う場合,このように線状スペクトルで計測できれば正確ですが,実際に,リアルワールドでこうした信号を扱う場合,なんらかの窓関数(信号を有限時間長に切り出す必要があるため)を介すため,様々な影響を受けています.
Rectangularの場合,上記3種の窓関数のなかで最もメインローブの幅が細い特徴があります.そのため被測定信号に含まれる成分の周波数の測定が最も精度良く得ることができます.
つづいてHanningは,メインローブの幅がRectangularほど細くはありませんが,サイドローブの減衰が大きいことが特徴です.この窓関数は信号に多くの周波数成分が含まれる場合,サイドローブの干渉が少なく各周波数成分の切り分けに優れています.
最後にFlattopは,名前の通りメインローブの頂上がフラットであることが特徴です.Rectangularのように先鋭なスペクトルの場合,周波数軸の計算幅の設定によって得られるF(ω)値が変化します.ちょうどピーク周波数をプロットした場合は正確にF(ω)の大きさを計算できますが,ピーク周波数から僅かでもずれればF(ω)は小さめに計算されてしまいます.
そこで,Flattopはメインローブの頂上がフラットである特徴によって信号に構成される周波数成分の振幅を精度良く測定することができます.また,F(ω)の大きさは,窓周期Tの大きさ(一般的には未知数)の影響を受けるため一般的には相対的な振幅測定となります.