電界2
仮にここで電界の大きさを単位面積あたりの電気力線の本数と決めます.このとき,あるポイントで1[m2] あたりの電気力線の本数が1本の場合,そこの電界は1[N/C] ということになります.これを関係式で示すとつぎのようになります.
![]()
図1-1-4 のケースで電気力線の本数を求めます.電界は点電荷を中心として距離r[m] における球面上ではどこでも同じ値になります.そこで,電気力線の通過する面積を半径r の球の表面積とします.S[m2] はその球の表面積になります.
![]()
よって電気力線の本数Φ は式1-1-4 に式1-1-3,式1-1-5 を代入して式1-1-6のようになります.
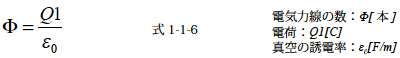
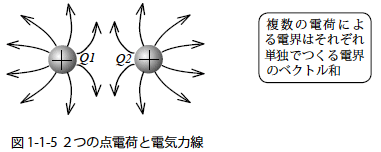
つぎに,図1-1-5 のように近接した2つの正電荷がつくる電界を考えます.
複数の電荷によってつくられる電界は重ね合わせの理 に従います.図1-1-5において合成される電界はQ1,Q2 がそれぞれ単独でつくる電界ベクトルを足し合わせた和になります.そのためQ1,Q2 が配置されるライン上においてお互いの電気力線が向かい合うところは相殺され電界が弱くなります.このときQ1,Q2 がつくる電気力線は本数の変化はなく分布のみが変わります.
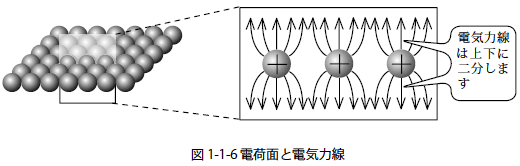
つぎに複数の電荷が平面状に配置されたときの電界を考えます.このとき電荷量は面に均等に分布しているものとします.図1-1-6 は広い平面電荷から一部を拡大したモデルです.面状に配置した電荷は,2つの点電荷による電界と同様,電荷間の空間は電界が相殺し弱くなります.そのため電気力線は図1-1-6 のように面に対し垂直方向に向かいます.そのため平面状の電荷による電気力線は平行でかつ均一な電気力線になります.