エミッタ容量(Cib)とスイッチング遅延

トランジスタにはコレクタ−ベース間，ベース−エミッタ間にＰＮ構成上，それぞれコレクタ容量（C_ob），エミッタ容量（C_ib）の静電容量が寄生することを説明しました（詳細こちら）．これら容量の存在によって，トランジスタの動作に与える影響を考えます．

ここでは，トランジスタのスイッチング機能とエミッタ容量C_ibとの関係について求めます．

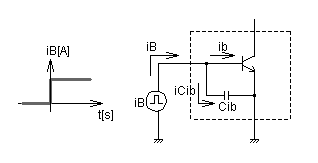
図3-3-16 C_ib分離の簡易モデルとシミュレーション系

図3-3-16は，ＮＰＮトランジスタのエミッタ容量とスイッチングの特徴についてのシミュレーション系で，ベース，エミッタ間に電流源i_Bを接続してステップ状の定電流を与えます．点線で囲んでいる部分を通常使用する一体の（寄生容量を含む）トランジスタとして想定します．

点線内部ではトランジスタに寄生するエミッタ容量（C_ib）を図のように分離して示すことにします．点線内中心に示すトランジスタは次の式3-3-4の関係のみ機能（電流増幅）を持つ簡易的なモデルとしてここでは考えることにします．

まず最初にエミッタ容量のみの影響について考えます．ここでは，コレクタ端を開放として考え，C_ob等コレクタ側の影響を排除してC_ibとi_bの関係を求めていきます．（ただし，コレクタ端に直流電源が接続されるなど，コレクタが交流的に接地される場合には，C_ibにC_obが並列接続されている状態と同様に考えることもできます．）

まず，ベース−エミッタ間電圧とi_bの関係について．この関係はPNダイオードのV_F−I_Fの関係（次の式3-2-5）と同様に考えることができます（詳細はこちら）．

つづいて電流源i_Bと各パラメータの関係は

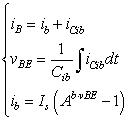式3-3-5

これら式3-3-5の関係をグラフに示すと

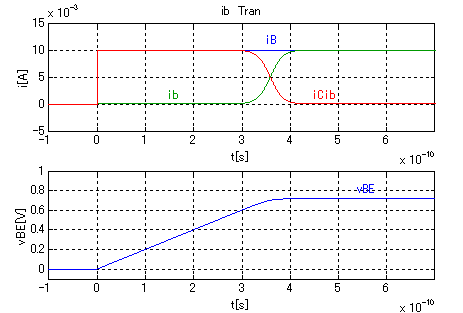
図3-3-17 ベース電流とエミッタ容量電流の関係 シミュレーション

＜参考＞シミュレーションM-fileはこちら

図3-3-17では，t=0[s]のときv_BE=0[V]と電圧が与えられていない条件で，i_Bにステップ状の電流を与えた際の，i_bおよびi_Cibの電流を計算しています．式3-2-5のi_bのv_BEに対する指数関数の関係からもわかるように，v_BEが小さい条件（i_Bステップ電流印可直後）ではi_bは流れにくく，i_B電流の多くはC_ibに充電電流として流れることになります．

時間経過とともに，C_ibが充電されv_BEの増加にともなってi_b電流が指数関数的に急激に増加を始めて，i_bがi_Bに漸近していきます．

もうちょっと簡単に考えれば，v_BEがPNの障壁電位に近づくとi_bが流れ出すことからも，C_ibの存在によってv_BEバイアス印可のためのC_ibの充電時間（遅延）が設定されることになります．図3-3-17の波形からも3×10^-10〜4×10^-10[s]のi_Bに対するi_bの遅延が容易に読みとれると思います．

この遅延時間は，C_ibの充電に要す時間すなわち

式3-3-6

TCib[s]:Cibによる遅延時間 ΔVBE[V]:vBEバイアス Cib[F]:エミッタ容量 iB[A]:ベース電流

C_ib 容量値に比例し，i_Bベース電流値に反比例します．

ただし，リニア領域で使用する場合デジタル用途に比べ，Δv_BEの電圧変動幅が小さくなるため遅延時間ΔT_Cibは小さいものとなります．