トランジスタの伝達関数モデル
トランジスタの数学的モデルについてエミッタ容量(Cib)を用いたモデルと,コレクタ容量(Cob)を用いたモデルのそれぞれを別々に求めてきました.ここでは,これらエミッタ容量(Cib)とコレクタ容量(Cob)両方の影響を考慮してトランジスタの数学的なモデルを求めたいと思います.
一般に,トランジスタの用途を大別するとリニア領域で使用する場合と飽和領域で使用する場合の2通りになります.この記事では,リニア領域での使用を前提に話を進めます.
後者の飽和領域に関しては,エミッタ容量(Cib)の影響によるスイッチング遅延はこちら.コレクタ容量(Cob)と立ち上がり時間の関係はこちらで説明しています.
両者は,お互いへの影響は小さくそれぞれ独立して遅延を計算できます.エミッタ容量(Cib)の影響によってスイッチング遅延している状態ではコレクタ電流がほとんど流れず,コレクタ電流が流れはじめてからコレクタ容量(Cob)が影響し始めます.そのため両者の遅延時間は,ほぼ直列に考えることができます.
エミッタ容量(Cib)とコレクタ容量(Cob)の単独での簡易モデルと伝達関数は下図の通りです.これら等価の根拠はそれぞれのページを参照してください.
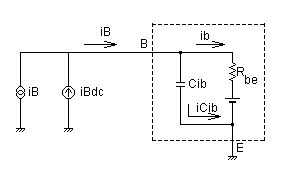
| エミッタ容量(Cib)と等価モデル |
 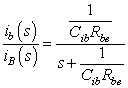 式3-3-8 式3-3-8
|
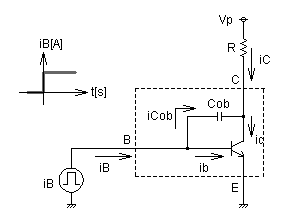
| コレクタ容量(Cob)と等価モデル |
 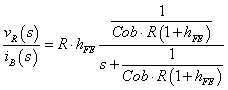 式3-3-12 式3-3-12
|
これらの系を合成して図示すると図3-3-28のように図示できます.
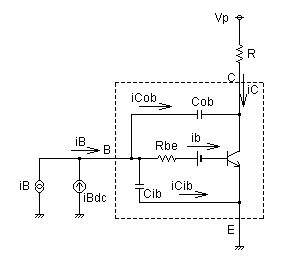
図3-3-28 エミッタ容量(Cib)とコレクタ容量(Cob)を含むトランジスタの系
図3-3-28は,トランジスタのコレクタに抵抗Rを介して直流電源Vpを接続し,ベース極に電流信号源iBと,直流電流源iBdcを接続した系です.直流電流源iBdcはトランジスタにバイアス電流を与えます.そしてさらにバイアス電流に加えてiBの信号電流を与えます.
点線部をエミッタ容量,コレクタ容量を含むトランジスタの簡易モデルとし,点線内部に記載されているトランジスタをBE間のインピーダンスを0Ωとし,次の式3-3-4の関係のみを持つ数学的モデルと仮定します.
バイアス電流iBdcが一定でこのバイアス電流に対して信号電流iBが充分小さい場合,一般にRbeを一定値として考えることができます(詳細説明はこちら)
| ic=hFE ib | 式3-3-4 |
ib:ベース電流[A] ic:コレクタ電流[A] hFE:直流電流増幅率[倍] |
図3-3-28から得られる関係は,
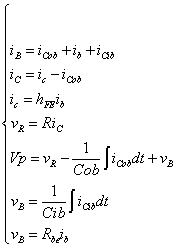
|
式3-3-17 |
Cob:コレクタ容量[F] Cib:エミッタ容量[F] rbe:BE間内部抵抗[Ω] ib:内部ベース電流[A] ic:内部コレクタ電流[A] iB:ベース電流[A] iC:コレクタ電流[A] R:コレクタ側抵抗[Ω] Vp:直流電源[V] vR:抵抗端電圧[V] hFE:直流電流増幅率[倍] |
式3-3-17から(計算過程はこちら)
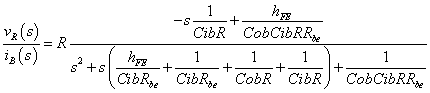
この伝達関数は右上の伝達関数計算ツールでシミュレーションできますのでご利用ください.