コレクタ容量(Cob)と立ち上がり時間
トランジスタは,コレクタ−ベース間,ベース−エミッタ間に,それぞれコレクタ容量(Cob),エミッタ容量(Cib)の静電容量が寄生します.ここでは,コレクタ容量(Cob)の存在によってトランジスタの電流増幅機能に与える影響を考えます.
そこで,下図のような系を使って,コレクタ容量(Cob)の寄生するトランジスタを簡易的な数学的モデルとして捉えます
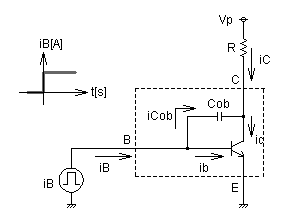
図3-3-23 コレクタ容量Cobと系
図3-3-23は,トランジスタのコレクタに抵抗Rを介して直流電源Vpを,ベース極に電流源iBを接続した系です.点線部をコレクタ容量を含むトランジスタの簡易モデルとし,点線内部に記載されているトランジスタを次の式3-3-4の関係のみを持つ数学的モデルと仮定します.(コレクタ容量のみの影響を抽出して考えます)
| ic=hFE ib | 式3-3-4 |
ib:ベース電流[A] ic:コレクタ電流[A] hFE:直流電流増幅率[倍] |
図3-3-23の系から各パラメータの関係は
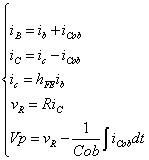 |
式3-3-11 |
Cob:コレクタ容量[F] ib:内部ベース電流[A] ic:内部コレクタ電流[A] iB:ベース電流[A] iC:コレクタ電流[A] R:コレクタ側抵抗[Ω] Vp:直流電源[V] vR:抵抗端電圧[V] hFE:直流電流増幅率[倍] |
ここからiBとvR の関係は(計算過程はこちら)
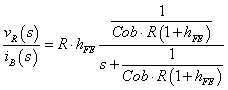
|
式3-3-12 |
Cob:コレクタ容量[F] iB:ベース電流[A] R:コレクタ側抵抗[Ω] Vp:直流電源[V] vR:抵抗R端電圧[V] hFE:直流電流増幅率[倍] |
式3-3-12vR(s)/iB(s)はベース電流に対する抵抗R端電圧の伝達関数を示します.この系はCR Lowパスフィルタなどの系と同様一次遅れの系になります.この伝達関数の計算は右記のツールによって試算できますのでご活用ください.
ここで,iB(s)にステップ状の電流を与えたときの,vR(s)の過渡応答の例を図3-3-24に示します.
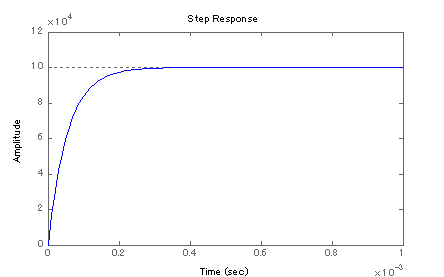
図3-3-24 vR(s)/iB(s)のステップ応答
図3-3-23の系を,スイッチとして使用する場合の遅延を考えます.
一般にスイッチとして設定する場合,on時に飽和させコレクタ電流ICは,およそVp / Rに張り付けます.(ただし,図3-3-24の波形は,飽和しない前提でリニア領域のみのシミュレーションをしています.)
そのため,一般にスイッチ用途における立ち上がり時間は,式3-3-12の伝達関数に設定される R(hFE+1)Cob の時定数の影響だけではなくVpも考慮する必要があります.
式3-3-12のステップ応答過渡関数は(計算過程はこちら)(一次遅れ伝達関数の逆ラプラス変換の解説)
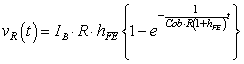
|
式3-3-13 |
Cob:コレクタ容量[F] R:コレクタ側抵抗[Ω] Vp:直流電源[V] vR:抵抗R端電圧[V] IB:ベース電流[A] hFE:直流電流増幅率[倍] |
立ち上がりに必要な時間は,vRが0[V]からVp[V]までの時間なので(計算過程はこちら)
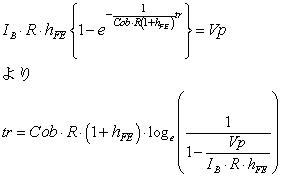
|
式3-3-14 |
Cob:コレクタ容量[F] R:コレクタ側抵抗[Ω] Vp:直流電源[V] IB:ベース電流[A] hFE:直流電流増幅率[倍] |
トランジスタの立ち上がり時間の設定には,式3-3-14を使うと便利です.一般的に立ち上がり時間を,0%→90%や 10%→90%や 5%→95%など仕様を様々に設定している場合がありますので,Vpに各率をかけてtrをそれぞれ算出して目的の立ち上がり時間を求めましょう.
さらにエミッタ容量Cibによる遅延も考慮する必要があります.エミッタ容量Cibによる遅延はコレクタ電流が流れる以前の遅延なので,スイッチング遅延に関してシリーズに考えることができます.