2次伝達関数とフィルタ特性
これまで2次系伝達関数の特徴を,次の式2-3-30のような2次系伝達関数の一般式を例にとり,その分母に着目して解説してきました.2次系伝達関数の分母は,振動の大きさや,その振動の周波数などを数学的に設計・解析できます.
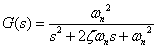 |
式2-3-30 |
このページでは,伝達関数の分子に着目していきます.伝達関数は数学上の問題ですので,本来は数学的に解決していくのが望ましいかもしれませんが,ここでは次表2-3-5に示すよう,R,L,Cを組み合わせた具体的な伝達系を例示して物理的なイメージを持ちながら考えていきたいと思います.
| 名称 | 系と伝達関数と周波数特性 |
| LPF |
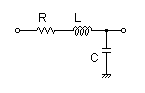
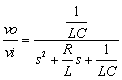
L=100uH C=220uF R=1.3Ω
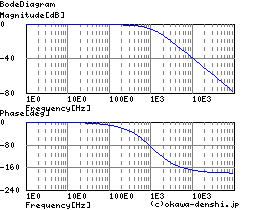 図2-3-28 |
| HPF |
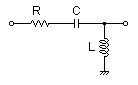
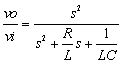
L=100uH C=220uF R=1.3Ω
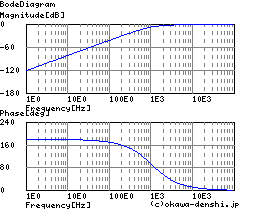 図2-3-29 |
| BPF |
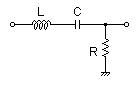
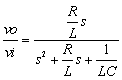
L=100uH C=220uF R=1.3Ω
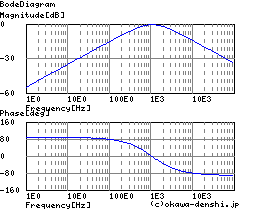 図2-3-30 |
| BEF |
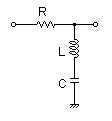
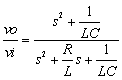
L=100uH C=220uF R=1.3Ω
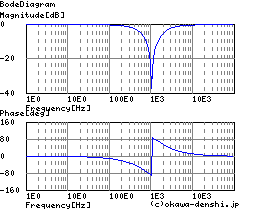 図2-3-31 |
表2-3-5 各種フィルタ系と伝達関数
表2-3-5の4例は,受動部品で構成する各種フィルタ回路と伝達関数です.上からローパス・フィルタ(LPF),ハイパス・フィルタ(HPF),バンドパス・フィルタ(BPF),バンドエリミネーション・フィルタ(BEF)となります.
いずれのフィルタも,パラメータは同様に設定しています.(L=100uH C=220uF R=1.3Ω)この設定は固定周波数(カットオフ周波数)がおよそ1KHz,減衰比がおよそ1(Qがおよそ0.5)になります.
表2-3-5の4系はR,L,C直列接続の系に信号を入力して,出力には,R,L,Cいずれかの部品(あるいはその組み合わせ)端の電圧を取り出すシンプルな系です.ここで4系の伝達関数を見るといずれも分母が同じになり,分子だけが異なることに着目します.
そこでまず,これらすべてのフィルタに共通に流れる電流について求めてみましょう.
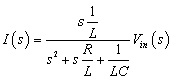
|
式2-3-45 |
R:抵抗[Ω] L:インダクタンス[H] C:静電容量[F] |
(式2-3-45の導出に関しては,こちらに類似例がありますので参照してください).式2-3-45をみると既にすべてのフィルタ伝達関数に共通の分母を備えています.伝達関数の分母は前に述べている通り,振動の大きさや固定周波数が設定されています.電流の伝達関数にこれらが織り込まれている点は物理的には腑に落ちるところかと思います.
式2-3-45の周波数応答を示すと次の通りです.
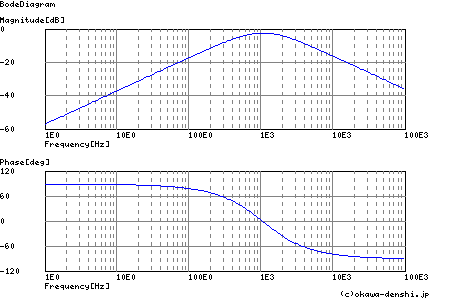
図2-3-32 RLC直列回路におけるI(s)/V(s) 伝達関数
図2-3-32の電流は,固定周波数(カットオフ周波数)となる1KHzを境にして低周波側で位相が+20dB/decadeのゲイン傾き,90[deg]の位相進みから微分機能を持ち.反対に高周波側で位相が-20[dB/decade]のゲイン傾き,90[deg]の位相遅れから積分機能を持つ特徴が図2-3-32から見てとれます.つぎの式2-3-45(変形)からも同様に考えることができます.
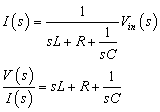
また,RLC直列の系ですからこの系に流れる電流は,低周波域では C によりインピーダンスが大きくなり,高周波域では L により やはりインピーダンスが大きくなります.そして,中周波域では,LC のインピーダンスが最も小さくなるピークの周波数が存在します.その周波数が固定周波数(カットオフ周波数)となります.よってこのRLC直列系に流れる電流は,既にバンドパス・フィルタの特徴をもっているのです.
つづいて,このフィルタ電流(式2-3-45)I(s) から各部品端の電圧を求めてみましょう.
| 部品 | 時間関数 | ラプラス関数 |
| L | 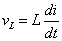 |
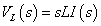 |
| R | 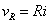 |
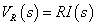 |
| C | 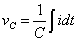 |
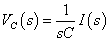 |
表2-3-6 RLC直列回路における各部品の電圧
時間関数をみるとRLC直列回路の電流 I(s) に対して,コイルが微分,抵抗が比例,コンデンサが積分に対応しています.物性から考えれば当たり前ですが,伝達関数の周波数応答においては重要な意味を持ちます.
表2-3-6のラプラス関数を式2-3-45 I(s)を導入して計算を進めると,VLはHPF,VRはBPF,VCはLPFの各伝達関数になります.ちなみにBEFはVL+VCに対応します.
表2-3-6のラプラス関数をみれば,微分,比例,積分がそれぞれs1,s0,s-1として微分演算子が変換されています.各フィルタの入力電圧に対する出力電圧の伝達関数においては,I(s)/Vin(s)伝達関数の分子にs項(のみ)があることから,上記の微分,比例,積分は,それぞれこの s が掛けられs2,s1,s0の各項に対応することになります.
伝達関数分子へのs2,s1,s0の配置による機能は表2-3-5に示す通りです.
2次フィルタは2次伝達関数の機能をそのまま利用した補償器です.反対に言えば,2次伝達関数もまた,機能・特徴は2次フィルタそのものです.ここであえて数学的に解釈すれば,LPFはカットオフ周波数より大きい高周波域で2次の積分器に等価的に機能し,HPFではカットオフ周波数より小さい低周波域で2次の微分器に等価的に機能します.また,BPFについては上で述べた通り,式2-3-45のバンドパス特性が抵抗による比例ゲインを介して出力されます.BEFは以前零点に関して同回路を使って解説していますので割愛.詳細はこちら