トランジスタの利得帯域幅積
一般的に利得帯域幅積とは,増幅器の性能を示す指標として使用されます.増幅器の信号増幅を対象とする周波数帯域において,任意に選ぶ周波数をf [Hz]としたとき,その周波数f における利得をG[倍]としたとき,G×f で計算される値が利得帯域幅積です.利得帯域幅積はGB積とも言います.単位は[Hz],[rad/s]などを使用します.
利得帯域幅積の値が大きい場合,低いものと比較して同周波数では利得が大きく,また,同利得では周波数が高く設定が可能で,増幅器の性能としては高いものになります.
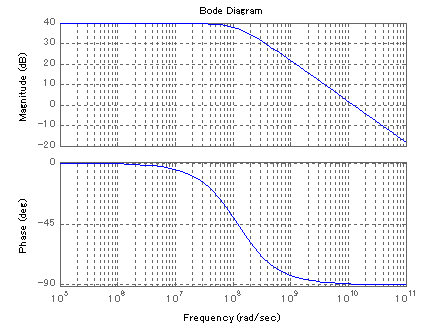
図3-3-21 hFE周波数特性の例
図3-3-21はトランジスタのhFE周波数特性の例を示しています.この特性のように,トランジスタの場合,高周波側でのhFE減衰域があります(図3-3-21の場合,108[rad/s]以上).トランジスタの利得帯域幅積は,一般にこの領域における任意の周波数f と,その周波数における利得をGとしたときの両者の積f ×G[Hz]で示されます.
トランジスタのhFEは,一次遅れの伝達系(詳細はこちら)であることから,利得の減衰傾きは-20dB/decade(-20dBは0.1倍,decadeは,たとえば10Hz〜100Hz,1kHz〜10kHzのように10倍の周波数間)となる特徴があります.そのため,トランジスタのような一次遅れの伝達系の増幅器の利得帯域幅積(f ×G)は減衰域でほぼ一定となります.
そのため,単純にhFEが0[dB]となる周波数(f [Hz]×1[倍])と一致します.
つづいて,トランジスタの利得帯域幅積とiB信号周波数との関係を考えます.
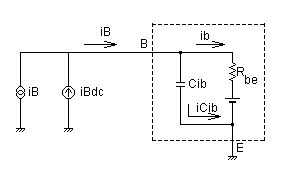
図3-3-20 ベース−エミッタ間の抵抗モデル
図3-3-20において,これまで次の関係を求めてきました.
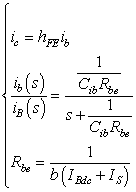 |
式3-3-4 式3-3-8 式3-3-7 |
ic:コレクタ電流[A] hFE:直流電流増幅率[倍] Rbe[Ω]:ベース−エミッタ間抵抗値 Cib[F]:エミッタ容量 iB[A]:ベース電流 ib[A]:Cib電流除くベース電流 IS[A]:飽和逆方向電流 b[V-1]:温度に係わる係数 |
上式の関係を踏まえ (上式の説明はリンク参照)
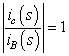 |
式3-3-9 |
ic:コレクタ電流[A] iB[A]:ベース電流 |
利得帯域幅積はベース電流iBのicに対する電流増幅率が0[dB]なので,式3-3-9の条件となる周波数ωを求めると
| |
式3-3-10 |
ic:コレクタ電流[A] hFE:直流電流増幅率[倍] Cib[F]:エミッタ容量 iBdc[A]:ベース電流バイアス IS[A]:飽和逆方向電流 b[V-1]:温度に係わる係数 |
ここでベース−エミッタ間抵抗Rbeを式3-3-10に代入して求めます.
Rbeは式3-3-7に示すとおりですが,実際のRbeは,利得帯域幅積に近いところで高周波の領域になり,表皮効果の影響によって式3-3-7の関係に示す抵抗値よりも大きくなります.
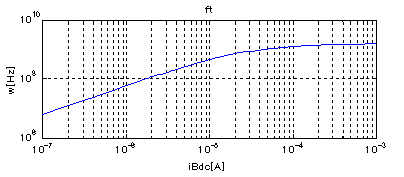
図3-3-22 ベース電流バイアスと利得帯域幅積の関係
図3-3-21は,その表皮効果による補正を考慮してベース電流バイアスと利得帯域幅積の関係を示しています.縦軸が利得帯域幅積です.
ベース電流バイアスの小さい状態では,式3-3-7に示すようにRbeが大きくなります.そのためエミッタ容量とのCRの時定数が大きくなり,hFE減衰が低い周波数から始まります.そのような影響で利得帯域幅積は,ベース電流バイアスが小さいほど小さくなります.
反対にベース電流バイアスの大きい状態では,式3-3-7に示すようにRbeが小さくなります.しかし,一般にトランジスタの利得帯域幅積は周波数が高く,この高周波の影響によって,Rbeが表皮効果によって抵抗値が高くなります.この高周波では表皮効果によるRbeの大きさが支配的になり利得帯域幅積が飽和します.
図3-3-21のグラフは,図3-3-20におけるic/ibの(式3-3-4に示す)hFEを一定として算出しています.しかし,実際のトランジスタのhFEは一定ではなくエミッタ(コレクタ)電流の影響を受けます.
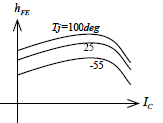
図3-3-12 hFE−Ic 特性
図3-3-12は,hFEとコレクタ電流の一般特性を示しています.hFEは,この特性図のようにエミッタ(コレクタ)電流の大きい領域ではキャリア飽和による影響を受け低下します.
このようにエミッタ(コレクタ)電流の影響を踏まえると,ベース電流バイアスと利得帯域幅積の関係についても,ベース電流バイアスが大きくなる領域では,利得帯域幅積が低下します.(図3-3-21のグラフには反映していません.)