ラプラス変換の利点

これまでにＣＲ回路の過渡現象についての微分方程式を，そのまま微積をつかって解く方法と，ラプラス変換によって解く方法との２種類を示してきました．例題の微分方程式はそれ自体が単純なのでラプラス変換の利便性がわかりにくいかもしれませんが，もうちょっと微分方程式が高次になり複雑になってくると解くためにはかなりの重労働を強いられると思います．

図2-1-5はラプラス変換を使って微分方程式を解く際のシーケンスを示しています．

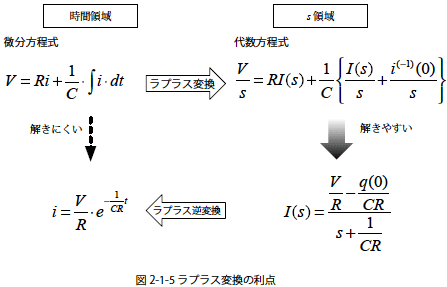
これまでに例を示したようにラプラス変換をすることによって，微分方程式のdtをラプラス演算子sに取り込んでしまうことができます．すると微分方程式であった原型は複素数s領域の代数方程式へと変化します．

この方程式から，もともとの微分方程式で得たいパラメータを，ラプラス演算子sを含む形で求めます．このとき当該パラメータを代数的に求めることができるため，微分方程式をそのまま解くよりは容易に解を得られるという利点があります．

こうして代数的に求められた解はs領域の解なので，再びラプラス逆変換を用いて時間領域に戻します．

こうした一連のフローによってかなり難解な微分方程式も（容易に？）解くことができます．ラプラス変換の利点はこの例のように微分方程式をsの代数方程式に変換して解きやすくする点にあります．

以前に述べたことと重複しますが，ラプラス変換の利点は微分方程式の解法にとどまらず，応用分野は多岐に及びます．回路設計の分野だけでも過渡現象，フィルタ設計，周波数解析，位相補正，フィードバック等制御分野など多くの利点にあずかることができます．

また，ラプラス変換を足がかりにフーリエ変換，Z変換，離散（デジタル）制御，FFT等測定技術，画像処理など裾野は広くラプラスを起点とする技術の体系から得られる恩恵は大きいと考えています．