ソレノイドのつくる磁界２

無限長ソレノイドのつくる磁束密度の求め方 解説　（続き）

つぎに微小電路群を環状に接続して無限長ソレノイドをつくります．このときソレノイドの断面形状は円である必要はありません．たとえば図1-5-5 のようなソレノイド断面電路C を考えます．

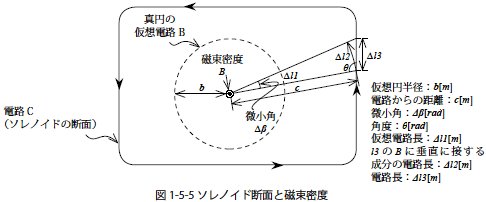
図の∆l3微小電路群がつくる磁束密度∆Bは式1-5-13より次のように示せます．

全電路によってつくるB は電路C に沿って積分すると次のように示せます．

つぎにこの式を図に示す真円の仮想電路B に等価変換します．

式中のsinθ·∆l3 は磁束密度B に対する垂直成分であるので∆β を0[rad] に限りなく近いものとすれば次の関係があります．

さらにb·∆l2=c·∆l1 なので

となります，従って∆β→0[rad] の極限値は式1-5-18 となります．

つぎに式1-5-15 に示した電路C に沿った積分を電路B に沿った積分に変換します．

この式に式1-5-18 を代入すると

となります．これを仮想円B の円周に沿って積分すると

と導くことができました．

つづいて無限長ソレノイドの外の磁束密度を求めます．先ほどと同様にソレノイドの外に真円の仮想電路を想定します．

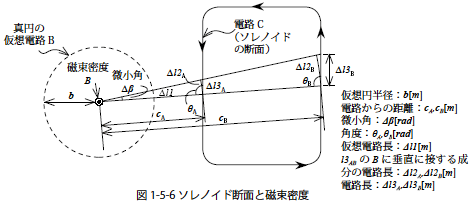
このとき仮想円中心の磁束密度は式1-5-13 より

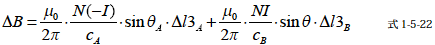
この式から先ほどと同様に仮想電路B に等価変換します．∆β を0[rad] に限りなく近いものとすれば前記の通り次の関係を示すことができます．

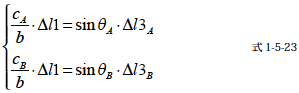
これらの式を式1-5-22 に代入すると

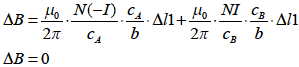
となり電路からの磁束は相殺され0[T] となります．また電路の無いその他の空間からは磁束の影響はないのでソレノイドの外における磁束密度B は

となります．