ソレノイドのつくる磁界
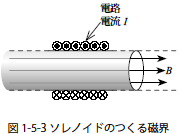
つぎに無限長ソレノイドのつくる磁界について考えます.ソレノイドは図のように円筒状に導線を巻いたコイルです.ソレノイド内部の磁束の方向はコイルを構成する電路一本一本に右ねじの法則を適用すると,コイル内の磁束は図1-5-3 に示すように同一方向に向かいます.また磁束の進行方向に対して電流の回転方向がこれも右ねじの法則に適合します.コイル内の磁束密度B はソレノイドの単位長さ(1m) あたりの巻き線数をN とすると
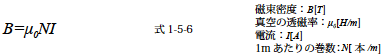
式1-5-6 のように示すことができます.無限長ソレノイド内部の磁束密度は上式に示すように巻き線の半径やコイル内の位置によらず一定となります.また,ソレノイド外部には磁束が発生しない特徴もあります.
無限長ソレノイドのつくる磁束密度の求め方 解説
無限長ソレノイドの内部および外部の磁束密度を求めます.最初に図1-5-4のように微小電路∆l が平行に複数配置された系のつくる磁束密度を考えます.微小電路はx 方向に単位長さ(1m) あたりN 本の間隔で均等に配置されます.微小電路に流れる電流は一本あたりI[A] とします.そのときy 軸上原点からaの距離の点の磁束密度∆B は原点から見て左右の電路のつくる磁束密度によってy 軸方向の成分は相殺されますので図のようにx 軸と平行に向かいます.
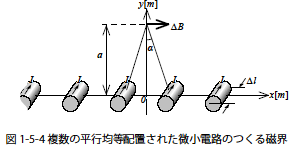
電路群の単位長さあたりの電流は∆x·NI です.この電流のつくる磁束密度∆Bはビオ・サバールの法則に従うと,式1-5-7 のように与えられます.

このときr およびx には次の関係があります.
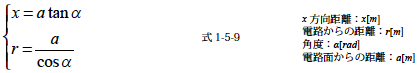
式1-5-7 をx について-∞ 〜 +∞ の範囲で積分することによって∆B を求めることができます.このときB のx 成分のみを抽出するのでcos α を掛けます.
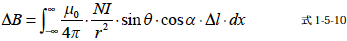
この式をα による積分に変換すると式1-5-11 のように示せます.このとき積分範囲は-π/2 〜 +π/2 となります.
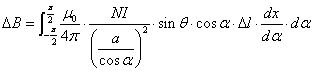 |
式1-5-11 |
式中の![]() は式1-5-9 を微分することで導くことができます.
は式1-5-9 を微分することで導くことができます.
![]()
式1-5-11 に式1-5-12 を代入して積分を解くと
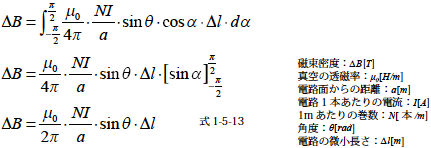
となります.
ソレノイドのY軸方向の磁界成分が相殺されること、そして、ソレノイド内の磁束密度が均一になることも理解出来るのですが、外側に磁界が出来ないということが釈然としません。
計算上、そうなるのは分かりますが・・・電路の作る磁界が円を描くのに・・・ソレノイドの外側に磁界が出来ないというのが理解に苦しみます。
【回答】2008/12/05
> 電路の作る磁界が円を描くのに・・・ソレノイドの外側に磁界が出来ない
おっしゃる通りです.ミソはこのソレノイドが無限長であるというところです.無限長というのは端を想定しませんので電路を回って磁束が一回転するという発想を持つことができません.両端がつながったソレノイドに近いイメージ(厳密には違いますが)を持ってもらうといいかもしれません.
たとえば,U字形永久磁石に,釘でもつければたくさん付きますが,同じU字形永久磁石を2個を環状に付ければ,釘はほとんど付くことはありません.電磁石(ソレノイド)についても同様です.こんな感じでイメージすれば良いのかなと思います.