コンデンサの合成
複数のコンデンサによって構成される回路または接続があるとき,任意の2点からみると一本のコンデンサとして等価的に扱うことができます.その等価コンデンサの静電容量は合成静電容量または単に合成容量と呼ばれます.
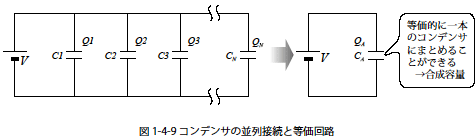
図1-4-9 は定電圧電源に複数のコンデンサを並列に接続した回路図です.この系の合成容量をCA[F] としたとき,回路を構成するコンデンサとの関係を求めます.図1-4-9 の系ではC1 〜 CN のコンデンサすべてに電源電圧V が与えられます.そのため回路を構成するx 番目のコンデンサをCx とすると,Cx に充電される電荷Qx はつぎのようになります.
| Qx=Cx·V | 電荷:Qx[C] 静電容量:Cx[F] 電圧:V[V] |
つぎに合成容量CA に充電される電荷は各コンデンサの充電電荷の和なので
QA=Q1+Q2+Q3+···+QN
QA=C1·V+C2·V+C3·V+···+CN·V
QA=(C1+C2+C3+···+CN)·V
QA=CA·V より合成容量CA は式1-4-20 のようになります.
CA=C1+C2+C3+···+CN
![]()
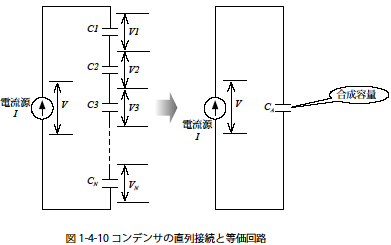
図1-4-10 は定電流源に複数のコンデンサを直列に接続した回路図です.この系の合成容量をCA[F] としたとき,回路を構成するコンデンサC1 〜 CN との関係を求めます.図1-4-10 のように直列に接続された系ではC1 〜 CN のコンデンサすべてに電流I が流れます.そのため回路を構成するx 番目のコンデンサをCx とすると,Cx の電圧Vx はつぎのようになります.
![]()
つぎに合成容量にかかる電圧V は各コンデンサ電圧の和なので
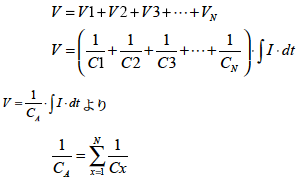
【質問】2008/07/09
コンデンサの直列接続は、理論としては上記式のごとくですが、現実には全体の耐電圧が上昇するので、使用可能な合成容量は上の式とは異なると思いますが、どうでしょうか?
【回答】2008/07/24
現実のコンデンサは,温度条件,経時劣化,力学的圧力や歪み,電圧などで静電容量は変化します. こういった条件変化の前後では,接続方法によらず個々のコンデンサの容量が変化しますので,全体の系の容量も変化することになります.
ただし,系に与えた条件の結果,個々のコンデンサ容量値がC1,C2・・・CNであることが確かな場合には, 本文記載の理論式に完全に従います.
コンデンサの直列接続は、理論としては上記式のごとくですが、現実には全体の耐電圧が上昇するので、使用可能な合成容量は上の式とは異なると思いますが、どうでしょうか?
【回答】2008/07/24
現実のコンデンサは,温度条件,経時劣化,力学的圧力や歪み,電圧などで静電容量は変化します. こういった条件変化の前後では,接続方法によらず個々のコンデンサの容量が変化しますので,全体の系の容量も変化することになります.
ただし,系に与えた条件の結果,個々のコンデンサ容量値がC1,C2・・・CNであることが確かな場合には, 本文記載の理論式に完全に従います.