平行極板の静電容量
図1-4-2 のような極板面積S[m2],極板間隙d[m] をもつ一対の平行極板によって構成されるコンデンサの静電容量C[F] を求めます.このコンデンサの充電電荷を電荷密度−単位面積(1m2)あたりの電荷量−で+σ,-σ[C/m2] とします.
そのときの平行極板の間の電界の大きさE を式1-4-3 に示します.(詳細は電界セクションの式1-1-8を参照)
![]()
極板間の電位と等電位面の位置の関係は式1-4-4 のようになります.ただし,等電位面位置は極板面と垂直の方向の距離をx[m] として,マイナス極板の位置を基準(x=0)とします.

極板間の電界は均一なので式1-4-4 は次のようになります.
| V = E・d | 式1-4-5 |
コンデンサの充電電荷Q[C] は電荷密度と極板面積より次のようになります.
| Q=σ・ S | 式1-4-6 | 電荷量:Q[C] 電荷密度:σ[C/m2] 極板の面積:S[m2] |
式1-4-3,式1-4-5,式1-4-6 より電荷Q[C] は
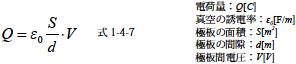
となります.Q=CV より平行極板の静電容量C[F] は次のようになります.
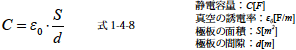
よって平行極板の静電容量は極板の面積に比例し,極板間隙に反比例する特徴があります.