抵抗によるアナログ電圧の加算
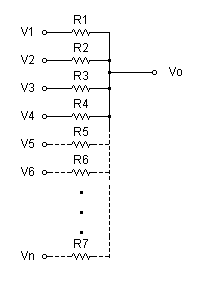
図1-2-13 アナログ加算回路
図1-2-13のように抵抗と電源だけで構成された回路について考えます.
この回路は,電圧 V1 からVn の低インピーダンス電源に抵抗を接続しただけの回路で,各電源の電圧をアナログ的に加算計算をします.
電子回路の設計でアナログ的要素を含む場合には,この回路が簡単な構成で,遅延が無く,経済的にも優れているので,よく 利用されます.
例えば,こちらの抵抗分圧回路や交流電圧のオフセット調整についても,このアナログ加算回路を利用・応用しているものです.
電圧Voについて,鳳- テブナンの定理を利用して求めてみようと思います.
テブナンの定理では,複数の抵抗と電源から構成される回路を,一本の抵抗と電源に仮想的に置き換えて考えることができますので,図1-2-13 のアナログ加算回路を図1-2-14 のように置き換えて Vo と Za について求めます.
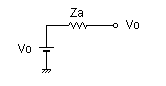
図1-2-14 抵抗回路の等価回路
テブナンの定理では,図1-2-14における Za は 回路網中のすべての電源を短絡状態と仮想して Vo からみた抵抗値になります.詳細は鳳- テブナンの定理を参照してください.
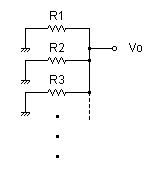
図1-2-15
テブナン定理による仮想電源短絡
そこで,すべての電源を仮想短絡した状態を図1-2-15に示します.この図より,Vo からみた抵抗値Zaは,R1 から Rn の並列に接続されている状態です.この合成抵抗を求めましょう.(並列抵抗の合成はこちらを参照下さい)
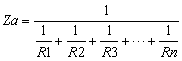
|
式1-2-21 |
つづいてVoを求めます.
Vo の計算では,図1-2-16のようにVo端子をGNDに接続した回路 において流れる電流を考えます.
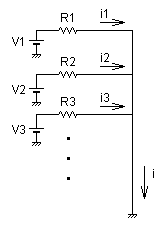
図1-2-16 GND接続時の電流
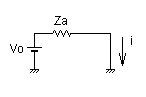
図1-2-17
V1〜Vnのすべて電源がGNDに流す電流の合成 i は,それぞれの電源から流れる電流 i1,i2,i3・・・in の合計なので 式1-2-22 のように現せます.
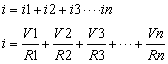
|
式1-2-22 |
図1-2-16のテブナン等価回路となる図1-2-17の電流 i は,オームの法則のままですので次の式1-2-23の通りです.
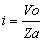
|
式1-2-23 |
式1-2-22 の i と式1-2-23の i とは同じ値ですので,これらの式より
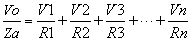
上式から Vo を求めると,式1-2-24のようになります.
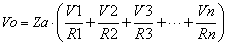
|
式1-2-24 |
ただし,
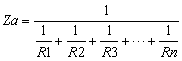
このようにV1〜Vnに係数が掛かった状態でのアナログ加算器を構成していることがわかると思います.