伝達関数の意義

これまで電子回路の特性を検証する方法として電圧・電流など回路上のパラメータについて過渡関数を求めたり，フーリエ変換をして周波数特性を得る方法を解説してきました．

電源投入時の過渡解析や，デジタル波形など過渡波形が常に一通りの場合には有効です．しかし，フィルタ回路のように入力波形に応じて，出力波形が得られるような開回路の場合，入力波形に応じて多様な過渡特性が得られるため，回路の特徴をとらえることは困難となります．

そこで，入力 → 出力間の信号伝達を示す伝達関数が回路検証としてよく用いられます．伝達関数は，電子回路の信号伝達の特性を数学的モデルとして示すもので，電子回路の本質的な機能・特性を抽象化します．

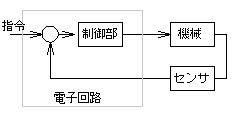
図2-3-1 複数の工学分野にまたがる制御系

一般に，図2-3-1のように複数の工学分野にまたがる系（電子回路を用いて機械を制御する場合など）があった場合，回路動作，機械動作を独自に検証するだけでは系全体の挙動を設計・検証することはできません．

そこで，それぞれを共通な数学上のパラメータにモデル化することで，もともと関係の無かった各工学分野のパラメータについて，数学的なコネクションをつくることができます．その共通モデルが伝達関数となります．

伝達関数は電子回路のモデル化のみではなく，機械系，化学系などについてもモデル化することができます．制御系全体の設計・検証を行う上で，伝達関数などの数学モデルは唯一無二の共通モデルといえます．