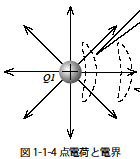
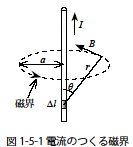
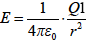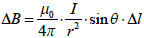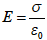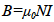電界と磁界のアナロジー
様々な物理法則はお互いに類似性のあるものがあります.たとえば重力,電気力,モノポール(磁荷)に適用される磁力などいずれもクーロン力に従います.こうした類似性をアナロジーといいます.
アナロジーの観点から電界と磁界について物理的な類似性や相違点の比較から電磁界の理解をさらに深めましょう.これまで説明してきているコンテンツから対応を表にまとめます.
| 電界 | 磁界 | |
| 微小単位のつくる場 |
|
|
| 面状電荷,電流のつくる場 | 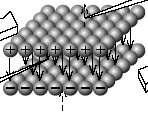
|
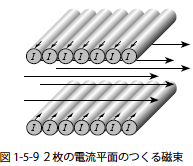
|
| 分極 |
|
|
| 空間のエネルギー | 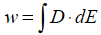 下記に解説 |
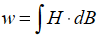 |
表1-6-1 電界と磁界の類似性
表1-6-1に示す関係より電界,磁界の対応するパラメータを抽出すると下表のようになります.
| 電界 E [V/m] | 磁束密度 B [A/m] |
| 電束密度 D [C/m2] | 磁界 H [A/m] |
| 電荷面密度 σ [C/m2] | 電流面密度 NI [A/m] |
| 電荷密度 ρ [C/m3] | 電流密度 J [A/m2] |
| 誘電率 ε [F/m] | 透磁率-1 1/μ |
表1-6-2 電界と磁界パラメータの対応
こうした対峙は物理的に大きな意味があるわけではありません(特殊な分野では意味を持ちます)が電界と磁界を理解する上で磁界の○が電界の△に対応しているとかを知っていると電界と磁界の相互の理解が促進すると筆者は考えます.
電界のエネルギーについての解説
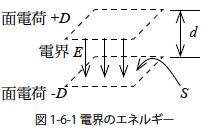
図1-6-1 に示す電界空間のもつエネルギーを求めます.
電界E [V/m]は均一であるものとし,その電界は均一に帯電した電荷密度D[C/m2] の電荷平面によりつくられるものとします.
平行極板に帯電した電荷Q [C]のもつエネルギーJ[J]は次のように示されます.
![]()
ここで電荷Q[C]およびv[V]は
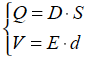
となります.V[V] はE[V/m]により微分し次のように変形します.
![]()
これを式1-6-1 に代入すると
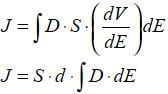
となり,この式から単位体積あたり(S・d=1m3)のエネルギーw[J/m3]を求めると
![]()
と導くことができます.