面状電流のつくる磁界

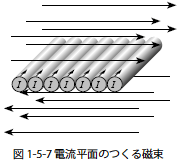
図1-5-7 のような無限長直線電流を∞本集合して構成する電流平面がつくる磁束の密度を考えます．構成される電路は単位長さ(1m) あたりN 本の間隔で均等に配置されます．電路に流れる電流は一本あたりI[A] とします．このとき電流平面の上下につくられる磁束密度は式1-5-25 のようになります．

無限長電流平面のつくる磁束は平面からの距離によらず均一になる特徴があります．これはちょうど電荷を平面状に配置するときにできる均等電界に対応する現象と考えることができます．

電流平面のつくる磁束密度の求め方 解説

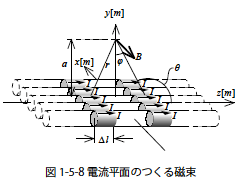
無限長電流平面のつくる磁束の密度Bを図1-5-8 のモデルで考えます．x 軸方向に均等に配置されている∆l の微小電路群がつくる磁界の磁束密度は式1-5-13 によって示されることを導きました．その式を使って微小電路群の電路をz 軸方向に±∞ [m] 延ばし電流平面をつくり磁束密度をz 軸方向に積分して磁束密度B を求めます．すると式1-5-26 のようになります．

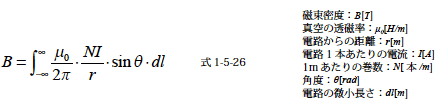
この式中のr，sinθ およびl を図1-5-8 より関係を示すと

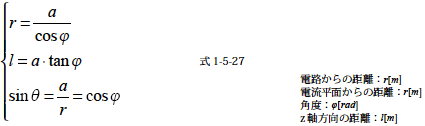
式1-5-26 のdl による積分をφ による積分に変換します．その場合，積分範囲は-π/2 〜 +π/2 となります．

式中のは式1-5-27 のl についての式を微分して導くことができます．

これを式1-5-28 に代入すると

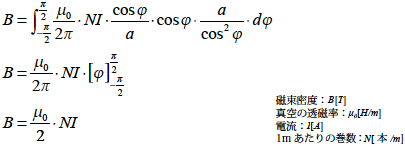
と導くことができました

電荷平面のつくる電界に対応させた磁束密度を図1-5-8 に示すような電流平面２枚（電流は反対方向）を重ねることによってつくられる磁束密度を考えます．このとき先に求めた１枚の電流平面がつくる磁束密度（式1-5-25）を重ね合わせること（ベクトル和）によって求めることができます．そこで式1-5-25 より

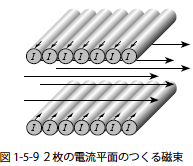
となります．これは先に求めた無限長ソレノイド内部および外部の磁束密度と同じです．

これに対応する２枚の異種電荷平面のつくる電界の強さは極板間は，極板外はE=0 の関係（式1-1-5参照）がありました．

これらの関係から磁束密度B と電界の強さE を対応させるとしたら，μ₀ とが対応しNI とσ が対応することがわかります．